Graphs of Elementary Trigonometric Functions
To see the functions in a clear manner, we’ll graph the trigonometric functions on the same graph as their reciprocals
This means that the ![]() curve and the
curve and the ![]() curve are graphed on the same graph.
curve are graphed on the same graph.
It also means that the ![]() curve and the
curve and the ![]() curve are graphed on the same graph.
curve are graphed on the same graph.
And finally, it means that the ![]() curve and the
curve and the ![]() curve are graphed on the same graph.
curve are graphed on the same graph.
Graph of:
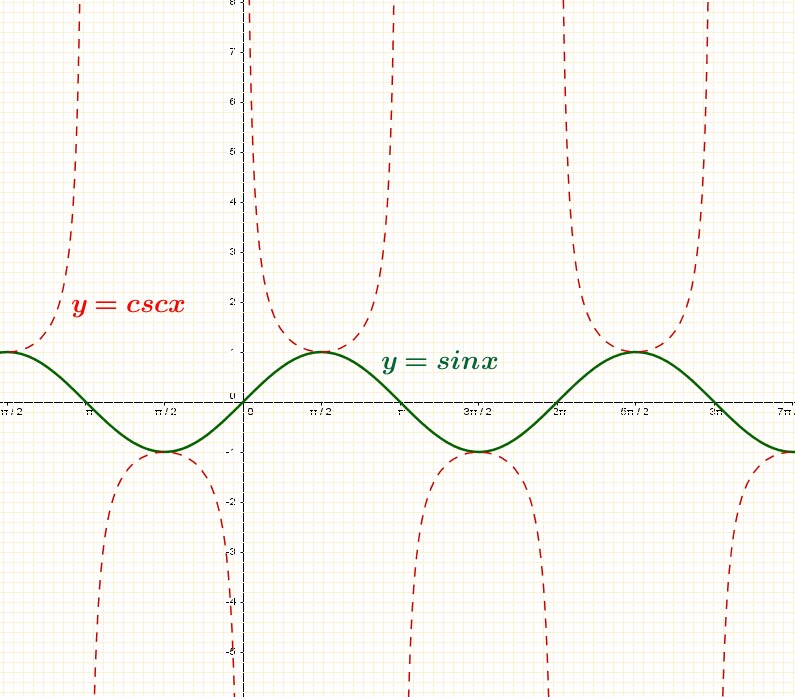
We notice that the two functions meet at the maximum and minimum values.
The function ![]() is not defined when
is not defined when ![]() . These are called the vertical asymptotes for the function
. These are called the vertical asymptotes for the function ![]()
Graph of:
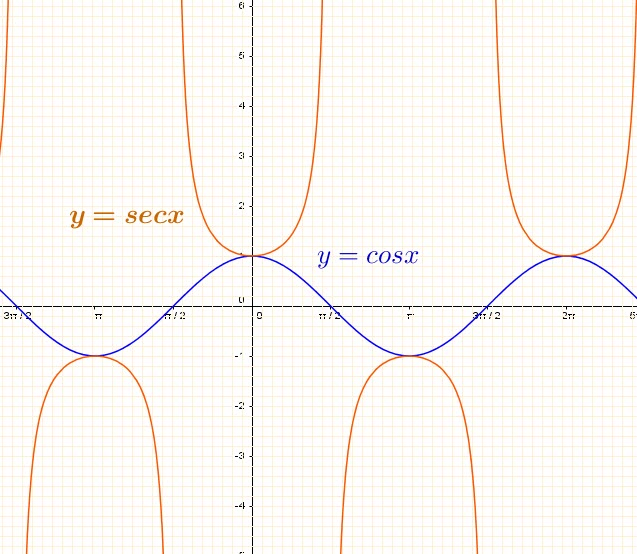
We also notice that the two functions meet at the maximum and minimum values.
The function ![]() is not defined when
is not defined when ![]() . These are again the vertical asymptotes for the function
. These are again the vertical asymptotes for the function ![]()
Graph of:
We also notice that the two functions intersect only when ![]() .
.
These points are multiple of a single angle when ![]() . Each function has an asymptote when the other function is
. Each function has an asymptote when the other function is ![]() .
.
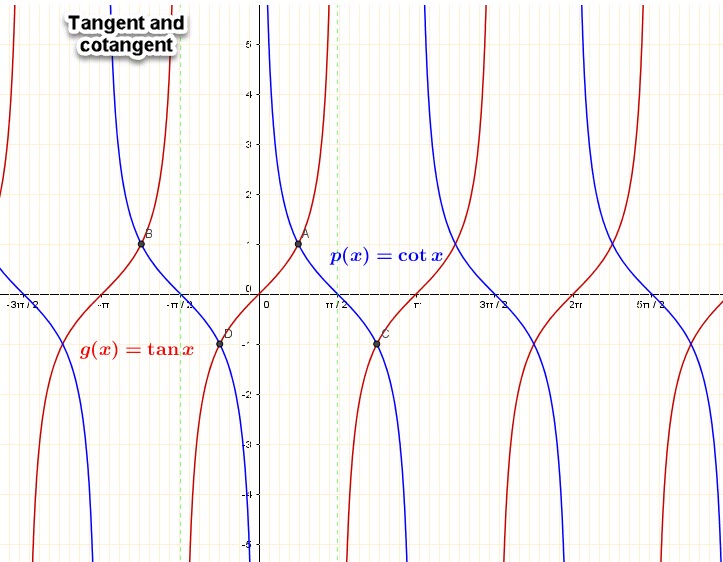
We can see in these graphs that each function resumes its pattern after some values of ![]() . They are said to be periodic.
. They are said to be periodic.
The repeated pattern is called a ![]() .
.
Let’s get a summary of the general behavior of these functions
The “sine” function:
With A,B,C and D being constants, we can see that we can easily graph this complex function using the base function of ![]() and the technics we learned from the quadratic functions.
and the technics we learned from the quadratic functions.
The Amplitude:
The amplitude ![]() is the measure of the maximum or minimum values from the midline
is the measure of the maximum or minimum values from the midline ![]() .
.
The amplitude itself is always positive. ![]() . The original
. The original ![]() is multiplied by
is multiplied by ![]() .
.
Period:
This is the horizontal width of a single cycle or wave. After this wave, the pattern repeats itself.
We can see that functions ![]() ,
, ![]() ,
, ![]() and
and ![]() repeat after
repeat after ![]() .
.
For the function:
![]() , we know that the period of the original/parent function
, we know that the period of the original/parent function ![]() is
is ![]()
The period of this function will be:
Frequency:
The frequency of the function is simply the reciprocal of the period.
The phase shift:
This is the horizontal shift of the original function and is calculated using:
The vertical shift:
The vertical shift is simply ![]()
All these values will be calculated the same way when we graph the function:
The period is useful when solving trigonometric equations.
For tangent and cotangent functions, we know that the period of the original/ parent function is ![]() .
.
The phase shift is important for the tangent:
![]() . The first cycle begins at the ‘zero’ that is “Phase shift units to the right of the origin”. The asymptotes are at
. The first cycle begins at the ‘zero’ that is “Phase shift units to the right of the origin”. The asymptotes are at ![]() to the left of the beginning cycle, and another at
to the left of the beginning cycle, and another at ![]() to the right of the beginning cycle.
to the right of the beginning cycle.
To graph 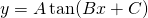 :
:
For nonzero real numbers ![]() and
and ![]()
-The period is ![]() and the phase shift is
and the phase shift is ![]()
Two consecutive asymptotes are found by solving:
![]()
The graphing is similar for the cotangent.
Example1:
Find the amplitude and the period of the function ![]()
In this function:
![]() and
and ![]()
The period ![]()
Example2:
![]()
Amplitude: ![]()
Period: ![]()
Example 3:
![]()
![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
The amplitude: ![]()
The period: ![]()
Phase shift: ![]()
The first interval is ![]() for a period of
for a period of ![]() .
.
Another way is to use the following rule:
The interval containing one cycle can be found by solving the following inequality:
![]()
We get:
![]()
![]()
Example 4:
Find the amplitude, period and phase shift of the following equation:
![]()
Amplitude:
![]()
Period: ![]()
Phase shift:
![]()
A sketch can be:
![]()


Be the first to comment