Quadrilaterals
Quadrilaterals
A quadrilateral is a polygon that has four sides. The line segment sides lie within a single plane.
Quadrilaterals with non-coplanar sides are called “SKEW”.
PARALLELOGRAM:
A parallelogram is a quadrilateral in which both pairs of opposite sides are parallel.
THEOREMS:
-A diagonal of a parallelogram separates it into two congruent triangles.
COROLLARIES:
-The opposite angles of a parallelogram are congruent
-The opposite sides of a parallelogram are congruent
-The diagonals of a parallelogram bisect each other.
-Two consecutive angles of a parallelogram are supplementary.
Theorems:
-In a parallelogram with unequal pairs of consecutive angles, the longer diagonal lies opposite the obtuse angle.
-If two sides of a quadrilateral are both congruent and parallel, then the quadrlateral is a parallelogram.
-If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
-If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
KITE:
The ![]() is a quadrilateral with two distinct pairs of congruent adjacent sides.
is a quadrilateral with two distinct pairs of congruent adjacent sides.
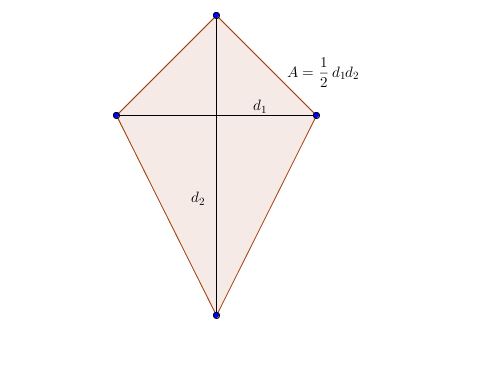
Theorem:
In a kite, one pair of opposite angles are congruent.
RECTANGLE, SQUARE AND RHOMBUS
A rectangle is a parallelogram that has a right angle.
COROLLARIES:
-All angles of a rectangle are right angles.
-The diagonals of a rectangle are congruent.
A square is a rectangle that has two congruent adjacent sides.
COROLLARIES
-All sides of a square are congruent
A rhombus is a parallelogram with two adjacent congruent sides.
COROLLARY:
All sides of a rhombus are congruent.
THEOREM:
The diagonals of a rhombus are perpendicular.
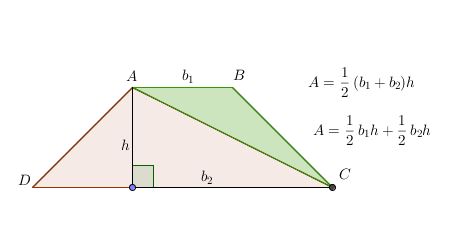
THE TRAPEZOID:
A trapezoid is a quadrilateral with exactly two parallel sides.
Theorems:
-The base angles of an isosceles trapezoid are congruent.
-The length of the median of a trapezoid equals one-half the sum of the lengths of the two bases.
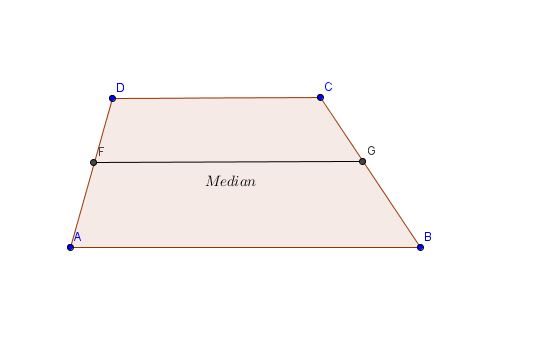
-The median of a trapezoid is parallel to each base
-If two base angles of a trapezoid are congruent, the trapezoid is an isosceles trapezoid.
-If the diagonals of a trapezoid are congruent, the trapezoid is an isosceles trapezoid.
-If three or more parallel lines intercept congruent line segements on one transversal, then they intercept congruent line segments on any traversal.
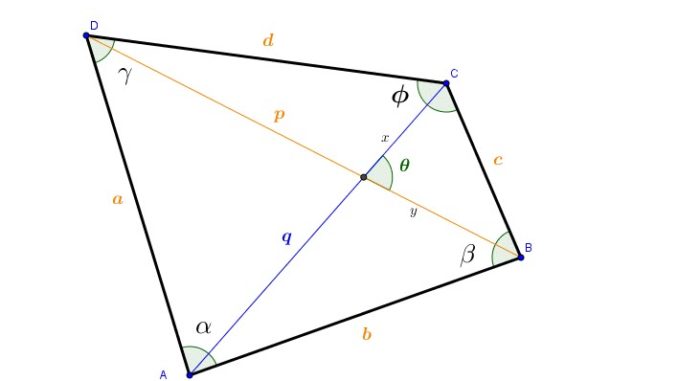
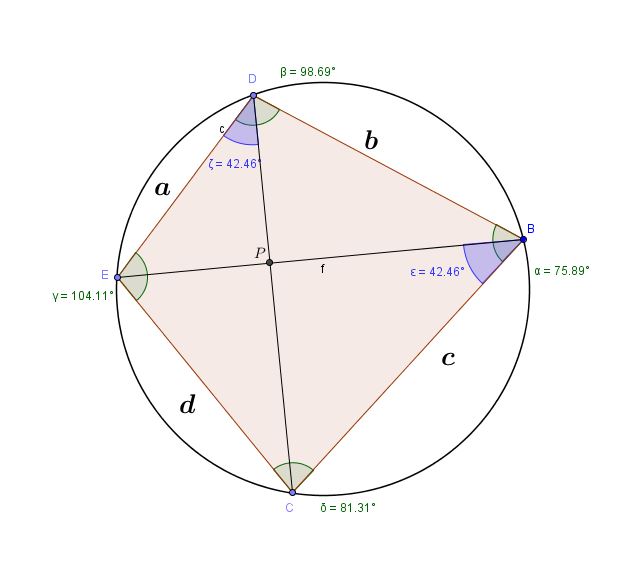
Cyclic Quadrilaterals:
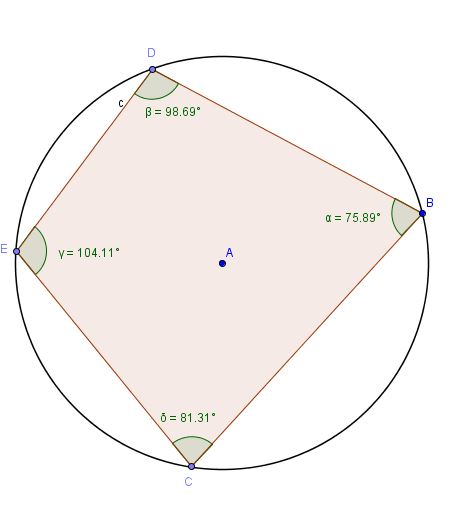
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle.
This means that the circle passes through all the four vertices of the quadrilateral.
Properties:
• The sum of the opposite angles of a cyclic quadrilateral is supplementary.
• The Perpendicular Bisectors of a quadrilateral are concurrent only if it is cyclic.
• The four perpendicular bisectors of the four sides meet at the center of the circle only if it is a cyclic quadrilateral.
• In a cyclic quadrilateral, the ratio of the diagonals equals the ratio of the sum of products of the sides that share the diagonal’s end points.
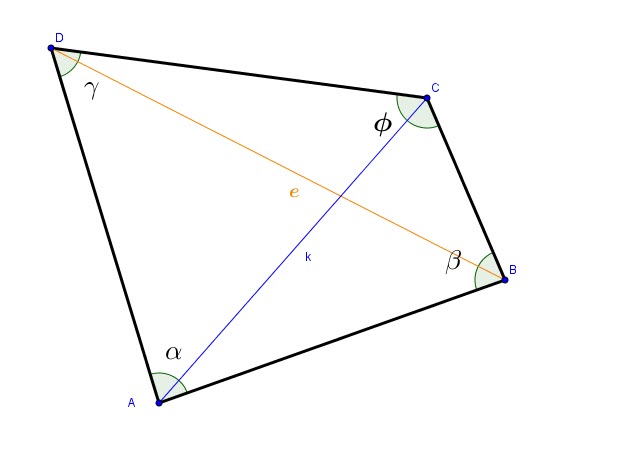
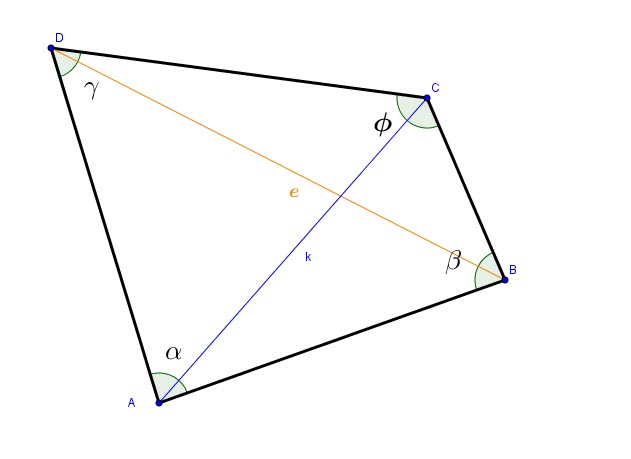
In a cyclic quadrilateral of sides a,b,c and d and of diagonals e and f:
Proof:
Let ![]()
In triangles ![]() and
and ![]()
![]()
But we know that:
Angles ![]() and
and ![]() are supplementary angles.
are supplementary angles.
That means: ![]()
We get:
![]()
![]()
![]()
![]()
Now back to the diagonal:
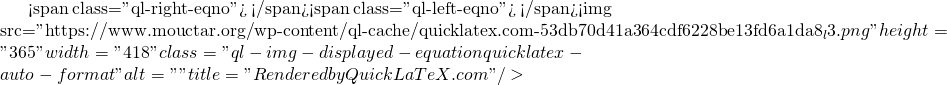
This yields:
![]()
Now let’s calculate ![]() :
:
In triangles ![]() and
and ![]()
![]()
But we know that:
Angles ![]() and
and ![]() are supplementary angles.
are supplementary angles.
That means: ![]()
We get:
![]()
![]()
![]()
![]()
Now back to the diagonal:
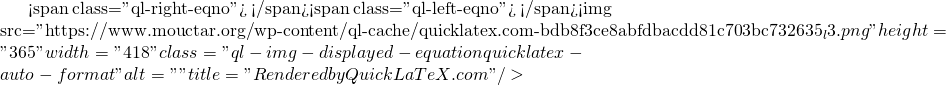
This yields:
![]()
Now Let’s calculate the product:![]() :
:
![]()
![]()
![]()
![]()
Finally:


Be the first to comment