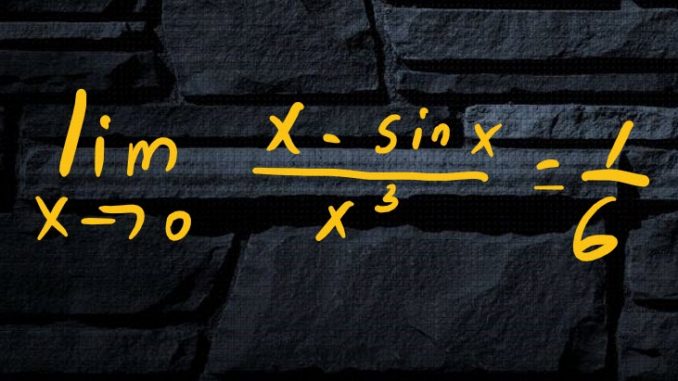
Higher order Derivatives
In the following formulas, we show the higher order derivatives before diving into practical applications.
If we define functions Like ![]() ,
, ![]() ,
,![]() and
and ![]() with
with ![]() being the variable and
being the variable and ![]() a natural number:
a natural number:
![]()
The chain rule:
![]()
This can be used to generate many formulas seen in our table.
Example:
![]()
Let ![]()
We know that:
![]()
![]()
Finally:
![]()
Logarithmic Differentiation:
This is a very useful method that can be used to find the derivative of any function.
Using the formula ![]()
We proceed as follows:
![]()
![]()
![]()
![]()
![]()
Example:
Find the derivative of:
![]()
Solution:
![]()
![]()
![]()
![]()
Second derivative
![]()
Higher-order derivatives
![]()
![]()
![]()
Leibnitz’s Formulas
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Some Applications of Derivative:
It will not be possible to list all applications of the derivative in few lines. However, through worked problems, this site will help you understand many aspects of the rate of change.
Remember that the derivative is the rate of change of some functions.
When you are driving a car, you start it, you accelerate and your speed increase at a certain rate. After some time, when you stop accelerating, you may drive at a constant speed. When you are near the point of arrival, you slow down and then stop.
The speed has increased, became constant and decreased. This is a typical derivative description. The rate of change was positive, so was the derivative during that period. Then the rate of change became ![]() and finally it became negative to the point of stop.
and finally it became negative to the point of stop.
Mean value theorem:
If a function ![]() is continuous on
is continuous on ![]() and differentiable on
and differentiable on ![]() , then
, then ![]() for some number
for some number ![]() in
in ![]() .
.
Corollary :
If ![]() for all
for all ![]() in
in ![]() , then
, then ![]() is constant on
is constant on ![]() , meaning that there is a constant
, meaning that there is a constant ![]() such
such ![]() for all
for all ![]() in
in ![]()
Corollary:
Let ![]() be a function that is continuous on
be a function that is continuous on ![]() and differentiable on
and differentiable on ![]() :
:
If ![]() for all
for all ![]() in
in ![]() , then
, then ![]() is an INCRESAING FUNCTION on
is an INCRESAING FUNCTION on ![]()
If ![]() for all
for all ![]() in
in ![]() , then
, then ![]() is an DECRESAING FUNCTION on
is an DECRESAING FUNCTION on ![]()
First derivative Test Theorem:
Let the function ![]() be continuous on the open interval
be continuous on the open interval ![]() and be differentiable there except possibly at
and be differentiable there except possibly at ![]()
1. If ![]() on
on ![]() and
and ![]() on
on ![]() , then
, then ![]() is the minimum value of
is the minimum value of ![]() on
on ![]()
2. If ![]() on
on ![]() and
and ![]() on
on ![]() , then
, then ![]() is the maximum value of
is the maximum value of ![]() on
on ![]()
3. If ![]() or
or ![]() for all
for all ![]() in
in ![]() except for
except for ![]() , then
, then ![]() is neither a maximum nor a minimum value for
is neither a maximum nor a minimum value for ![]()
Tangent line at a given point:
Normal line at a given point:
Inflection Points
If ![]() exists and
exists and ![]() changes sign at
changes sign at ![]() , the the point
, the the point ![]() is an inflection point of the graph of
is an inflection point of the graph of ![]() . If
. If ![]() exists at the inflection point, then
exists at the inflection point, then ![]()
L’Hopital’s Rule
![]()
if:
![Rendered by QuickLaTeX.com \[\lim_{x \to c} f(x)=\lim_{x \to c} g(x)=\begin{cases}0\\ \infty \end{cases}\]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-7e3a6890d9925d7c76044267e151d99c_l3.png)


Be the first to comment