Navigation and Trigonometry

Each point is identified by a pair of coordinates, the intersection of a meridian and a parallel.

The Latitude is the parallel. The Equator is the parallel located at $0^{\circ}$ . Moving North, the parallels North increase and at the North Pole $P$ , the latitude is $90^{\circ}\; North$ or $\frac{\pi}{2}$ .

Example $40^{\circ}\;N$

Moving South, the parallels South increase and at the South Pole, the latitude is $90^{\circ}\; South$ or $\frac{\pi}{2}$

Example $35^{\circ}\;S$

All parallel North of the Equator are in the Northern Hemisphere and the parallels south of the Equator are in the Southern Hemisphere.

The longitude is the Meridian. A notable meridian is the meridian passing through Greenwich. It is $0^{\circ}$ East or West.

Example of Meridians: $135^{\circ}\; West$ . The meridians are used to help mark the Time Zones.

As we said above, any point can be noted using its parallel and its meridian.

For a point $A$ :

If latitude is $20^{\circ}\;N$ and the longitude $45^{\circ}\; W$

We will note in this text:

$\varphi_{A}=20^{\circ}\;N$

$G_{A}=45^{\circ}\; W$

For a point $B$ :

If latitude is $35^{\circ}\;N$ and the longitude $65^{\circ}\; W$

We will note in this text:

$\varphi_{B}=20^{\circ}\;N$

$G_{B}=45^{\circ}\; W$

The term navigation here is the way to go from point $A$ to point $B$ , including Routes and distances.

We will discuss two types of sailing.

Rhumb Line Sailing: LOXODROMY

The rhumb line is represented on a map by a straight line on the Mercator projection. This is by no means the shortest distance between the two points on the sphere. The rhumb line however will have a constant route between the points.

The rhumb line, rhumb, or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true or magnetic north.

Rhumb lines which cut meridians at oblique angles are loxodromic curves which spiral towards the poles. On a Mercator projection the north and south poles occur at infinity and are therefore never shown.

If we have two points $A$ and $B$ not more than $375$ nautical miles, we will show the approximation formulas that can be used.

Let $m$ be the distance in nautical miles (1mile=1852 metres), $R_v$ the course or route in bearing, $\varphi_A$ , $G_A$ and $\varphi_B$ , $G_B$ the respective coordinates of points $A$ and $B$ .

We note:
The average latitude: $\varphi_m=\frac{\varphi_{A}+\varphi_{B}}{2}$

To the accuracy of 1 mile:

The Route:

$\tan {R_v}=\frac{G_B-G_A}{\varphi_B-\varphi_A}\cos {\varphi_m}$

The routes are counted from $N$ in a retrograde way. From $N$ we go to $E$ which is exactly at bearing $090^{\circ}$ and then to $S$ at bearing $180^{\circ}$ then to West $W$ which is at bearing $270^{\circ}$ and the we move to North $0^{\circ}$

The distance in nautical miles:

$m=\frac{\varphi_B-\varphi_A}{\cos {R_v}}$

Exact Formulas:

These take into account the increase of the latitude unit as we move away from the Equator.
They can be found using the GUDEMANN inverse function:
$\lambda=\ln \tan {\left(\frac{\pi}{4}+\frac{\varphi}{2} \right)}$

This is in radian and must be converted to minutes of arc.

The route

$\tan {R_v}=\frac{G_B-G_A}{\lambda_B-\lambda_A}$
If the base angle of the route is less than $89^{\circ}$ we use:
$m=\frac{\varphi_B-\varphi_A}{\cos {R_v}}$

If the base angle of the route is greater than $89^{\circ}$ , the tangent is no longer accurate. We use:

$m=-\frac{|(G_B-G_A)|\cos {\varphi_m}}{\sin {R_v}}$

Courses can be noted by their angle from axis of $NS$
Example:
$N65E=065^{\circ}$
$S65E=180-65=115^{\circ}$
$S65W=180+65=245^{\circ}$
$N65W=360-65=295^{\circ}$

Example:

A vessel steams a course $050^{\circ}T$ , for a distance of 500 miles from a departure position $\varphi_{1}=40^{\circ}25'S$ and longitude $G_{1}=175^{\circ}50'E$ .

Find the Latitude and the Longitude of the destination.

Solution:

The difference in latitude can be found from:

$m=\frac{\varphi_{2}-\varphi_{1}}{\cos {R_v}}$

$\varphi_{2}-\varphi_{1}=m\times \cos {R_v}$

$\varphi_{2}-\varphi_{1}=500 \cos {50}=321.4N=5^{\circ}21.4'N$

The destination Latitude:
$\varphi_{2}=40^{\circ}25'S+5^{\circ}21.4'N=35^{\circ}03.6'S$

For the longitude we use the exact formula:

$\tan {R_v}=\frac{G_2-G_1}{\lambda_2-\lambda_1}$
With:
$\lambda=\frac{180\times 60}{\pi}\ln {\tan {(45^{\circ}+\frac{\varphi}{2})}}$
We get:
$\lambda_1=\frac{180\times 60}{\pi}\ln {\tan {(45^{\circ}+\frac{40^{\circ}25'}{2})}}$
$\lambda_1=2655.4$
$\lambda_2=\frac{180\times 60}{\pi}\ln {\tan {(45^{\circ}+\frac{35^{\circ}3.6'}{2})}}$
$\lambda_2=2248.7$
$|\lambda_2-\lambda_1|=406.7$
The Difference in longitude:
$\tan {R_v}=\frac{G_2-G_1}{\lambda_2-\lambda_1}$
$G_2-G_1=406.7\times \tan 50=484.7=8^{\circ}04.7'E$ . Since the vessel is moving on an easterly course.
The final Longitude:
$G_2=175^{\circ}50'E+8^{\circ}04.7'E=183^{\circ}54.7'E$ But that is Western Longitude
$G_2=360-183^{\circ}54.7'=176^{\circ}05.3W$

Finally:
$\varphi_{2}=35^{\circ}03.6'S$
$G_2=176^{\circ}05.3W$

Parallel sailing

When the ship is moving between two points on the same latitude $\varphi$ , it is called PARALLEL SAILING.

The distance measured between meridians on the same parallel is called the DEPARTURE.

$Departure=DLong. \times \cos {(\varphi)}$

Example:
Find the distance between point of longitude $25^{\circ}45'W$ and point in longitude $50^{\circ}08'W$ on the same parallel $38^{\circ}50'N$

$DL=50^{\circ}08'W-25^{\circ}45'W=24^{\circ}23'=1463'$

The distance or Departure is:

$Dep=1463\times \cos {38^{\circ}50'}\approx 1140\;miles$

Exercise 1:

A ship sailed due west along the equator for 15 hours at a speed of 14 knots. Find her final position if her departure position was in longitude 11° 15’W.

Solution:

The departure along the parallel or distance:
$m=15 \times 14=210\; miles$
We know that:
$m=DL.\times \cos {\varphi}\Rightarrow DL.=\frac{m}{\cos {\varphi}}$
$DL.=\frac{210}{1}=210'=3^{\circ}30'W$

The final Longitude:
$11^{\circ}15'W+3^{\circ}30'W=14^{\circ}45'W$

Exercise 2:

Two freighters are 50 miles apart in the same parallel of $35^{\circ}N$
They both travel due South at the same speed until they are 60 miles apart.
What is their new latitude and what is the distance travelled by each.

Solution:

We know that the distance between the two freighters is:
$m_1=DL.\times \cos {\varphi_{1}}$
And
$m_2=DL.\times \cos {\varphi_{1}}$
Since both freighters are sailing due South, we can say that DL is constant.
$m_1=DL.\times \cos {\varphi_{1}}\Rightarrow DL.=\frac{m_1}{\cos {\varphi_{1}}}$
$DL.=\frac{50}{\cos {35^{\circ}}}$
$DL.=61.039$
The new Latitude:
$\cos {\varphi_{2}}=\frac{m_2}{DL.}$
$\cos {\varphi_{2}}=\frac{60}{61.039}$

$\varphi_{2}=10^{\circ}35.2'N$

The distance on due South or due North is simply the difference in Latitudes:

$Distance=35^{\circ}00.0'N-10^{\circ}35.2'N=24^{\circ}24.8'N=1464.8\;miles$

Exercise 3

A ship is in latitude $36^{\circ}18'N$ and travels due East True for 100 miles. She then sails $180^{\circ}T$ for 11 hours before turning West True and travelling for 100 miles. The ship finally heads north True and steams for another 11 Hours just to find herself 4 miles due East of her starting position.
How far South did she travel and what is the average speed if it is constant throughout the voyage while assuming that current and winds are negligible?

Solution:

Arriving 4 miles due east means to say that the actual DLong was not constant.
Making it constant here:
Assuming that she started at the arrival:
$m_1=DL.\times \cos {\varphi_{1}}$
$96=DL. \times \cos {36.3}$
$DL.=119.12$
When travelling 100 miles at another latitude with the same DLong:
$m_2=DL.\times \cos {\varphi_{2}}$
$\cos {\varphi_{2}}=\frac{100}{119.12}$

Lowest Latitude
$\varphi_{2}=32^{\circ}54.8'N$

The distance in the Southern track:
$m=36^{\circ}18'N-32^{\circ}54.8'N=3^{\circ}23.2'N=203.2\;miles$
Speed:
$203.2/11=18.47\;knots$

Great Circle Sailing: ORTHODROMY

Between points $A$ and $B$ on the sphere, the shortest distance is the orthodromy. The route following the great circle on the sphere.

The route is not constant here and at any given time we can get the initial course between the current point and the destination.

If the pole $P$ is on the North here, we can see that the three sides of the spherical triangle are as follows:

The distance AB noted $m$

The complementary angle to the latitude of $A$ this is $90-\varphi_{A}$

The complementary angle to the latitude of $B$ this is $90-\varphi_{B}$

The other elements:

$R_0$ is the initial course.

$DL$ is the difference in longitude.

We can use the spherical trigonometry formulas:

The Distance:

$\cos {m}=\sin \varphi_{A} \sin \varphi_{B}+\cos \varphi_{A} \cos \varphi_{B}\cos {DL}$

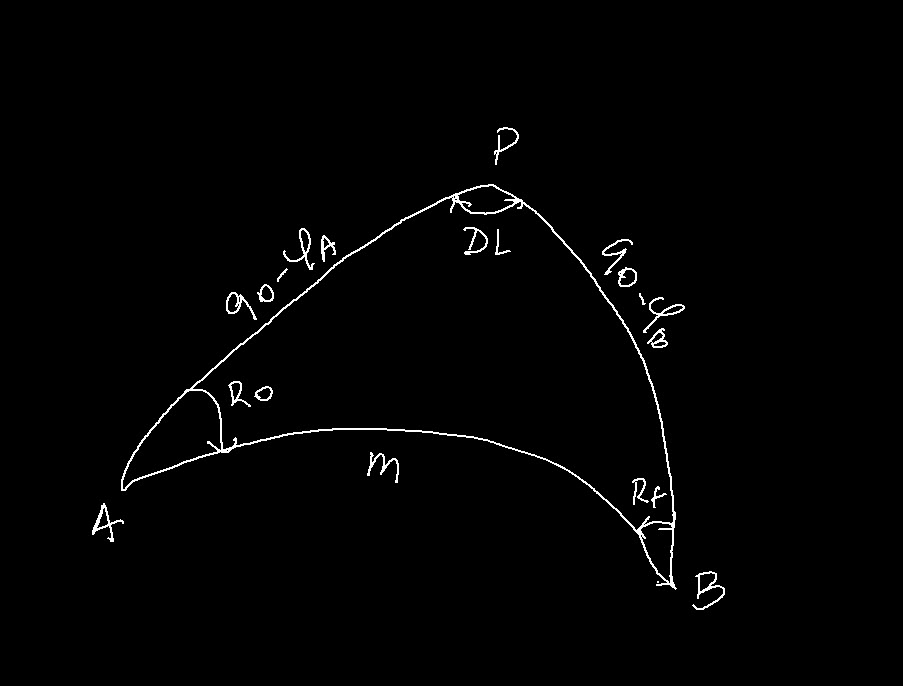
The initial Course:

In a typical GC sailing, the distance is split into daily distances and rhumb line courses are used between these waypoints.

The navigator may elect to alter course every 5 degrees of longitude or every 300 or so miles. The full path becomes a series of small rhumb lines.

The initial course can be computed by using the distance found in the formulas with arisk of errors or using other formulas.

From the figure we can see that:

$\cos (90-\varphi_{B})=\cos {m} \cos {(90-\varphi_A)}+\sin {m} \sin {(90-\varphi_A)} \cos {R_0}$

This makes it:

$\displaystyle{\cos {R_0}}=\frac{\sin {\varphi_B}-\cos {m}\sin {\varphi_A}}{\sin m \cos \varphi_A}$

Second method:

$\displaystyle{\cot {R_0}=\frac{\cos {(\varphi_A)} \tan {(\varphi_{B}})}{\sin {(G_B-G_A)}}-\frac{\sin {(\varphi_A)}}{\tan {(G_B-G_A)}}}$

Another formula:

$\displaystyle{\cot {R_0} =\frac{\cos {(\varphi_A)}\sin {(\varphi_B)}- \sin {(\varphi_A)}\cos {(\varphi_B)} \cos {(G_B-G_A)}}{\cos {(\varphi_B)}\sin {(G_B-G_A)}}}$

Another formula that can be used:

$\displaystyle{\sin {R_0}= \frac{\cos {(\varphi_B)}\sin {(G_B-G_A)}}{\sin {(m)}}}$

Vertex Coordinates:

There are two vertices and it is good practice to calculate the one in the direction of the initial Route.

The Orthodrome cuts the vertex meridian at a right angle:

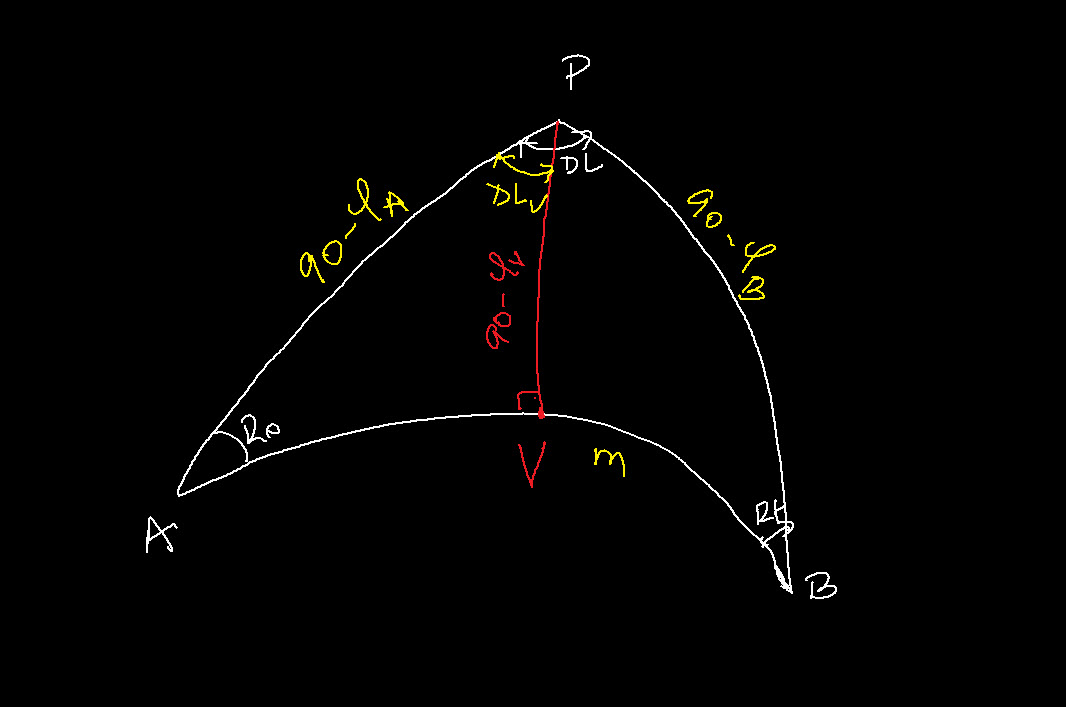
Using the Napier’s circle we can find:

The latitude of the vertex:

$cos {\varphi_V}=|\sin {(R_0)}|\cos {(\varphi_A)}$

The longitude of the vertex:

The difference in longitude from $A$ to $V$ :

$\cos {DL_V}=\frac{\tan {(\varphi_A)}}{\tan {(\varphi_V)}}$

Exercise 4:

A vessel plans to follow the Great Circle track between the two following points:

Departure
Latitude: $20^{\circ}52'S$
Longitude: $057^{\circ}37'E$

Destination:
Latitude: $32^{\circ}12'S$
Longitude: $115^{\circ}09'E$

Find the distance, the initial course and the final course.

Solution

The Difference in Longitude:
$Dl=115^{\circ}09'E-057^{\circ}37'E=057^{\circ}32'$ moving East

The distance:

$\cos {m}=\sin {\varphi_{1}}\sin {\varphi_{2}}+\cos {\varphi_{1}}\cos {\varphi_{2}}\cos {057^{\circ}32'}$
$\cos {m}=\sin {20^{\circ}52'}\sin {32^{\circ}12'}+\cos {20^{\circ}52'}\cos {32^{\circ}12'}\cos {057^{\circ}32'}$
$m=52.10193646^{\circ}$

The distance is:
$m=3126$ nautical miles

The initial Course:

$\cos {R_0}=\frac{\sin {\varphi_{2}}-\sin {\varphi_{1}}\cos {m}}{\sin {m}\cos {\varphi_{1}}}$
$\cos {R_0}=\frac{\sin {32^{\circ}12'}-\sin {20^{\circ}52'}\cos {52.10193646}}{\sin {52.10193646^{\circ}}\cos {20^{\circ}52'}}$

$R_{0}=S64.8^{\circ}E=115.2^{\circ}$

The final Course:

$\cos {R_f}=\frac{\sin {\varphi_{1}}-\sin {\varphi_{2}}\cos {m}}{\sin {m}\cos {\varphi_{2}}}$
$\cos {R_f}=\frac{\sin {20^{\circ}52'}-\sin {32^{\circ}12'}\cos {52.10193646^{\circ}}}{\sin {52.10193646^{\circ}}\cos {32^{\circ}12'}}$
$R_{f}=N92.5^{\circ}W\Rightarrow Final_{co}=087.5^{\circ}$

The Final Course:
$F_{co}=087.5^{\circ}$

Exercise 5:

A vessel taking the Great Circle track between the two following points:

Departure
Latitude: $38^{\circ}03'N$
Longitude: $122^{\circ}17'W$

Destination:
Latitude: $41^{\circ}30'N$
Longitude: $141^{\circ}13'E$

Find the distance, the initial course and the final course.

Solution

The Difference in Longitude:

$Dl=141^{\circ}13'E-122^{\circ}17'W=263^{\circ}30'$ moving East.
This being more than $180^{\circ}$
The vessel will move West:
$DL=360^{\circ}-263^{\circ}30'=96^{\circ}30'$ moving West.

The distance:

$\cos {m}=\sin {\varphi_{1}}\sin {\varphi_{2}}+\cos {\varphi_{1}}\cos {\varphi_{2}}\cos {96^{\circ}30'}$
$\cos {m}=\sin {38^{\circ}03'}\sin {41^{\circ}30'}+\cos {38^{\circ}03'}\cos {41^{\circ}30'}\cos {96^{\circ}30'}$
$m=70.023185^{\circ}$

The distance is:

$m=4201$ nautical miles

The initial Course:

$\cos {R_0}=\frac{\sin {\varphi_{2}}-\sin {\varphi_{1}}\cos {m}}{\sin {m}\cos {\varphi_{1}}}$
$\cos {R_0}=\frac{\sin {41^{\circ}30'}-\sin {38^{\circ}03'}\cos {70.023185^{\circ}}}{\sin {70.023185^{\circ}}\cos {38^{\circ}03'}}$

$R_{0}=N52.4^{\circ}W=307.6^{\circ}$

The final Course:
$\cos {R_f}=\frac{\sin {\varphi_{1}}-\sin {\varphi_{2}}\cos {m}}{\sin {m}\cos {\varphi_{2}}}$
$\cos {R_f}=\frac{\sin {38^{\circ}03'}-\sin {41^{\circ}30'}\cos {70.023185^{\circ}}}{\sin {70.023185^{\circ}}\cos {41^{\circ}30'}}$
$R_{f}=S56.4^{\circ}W\Rightarrow Final_{co}=236.4^{\circ}$

The Final Course:
$F_{co}=236.4^{\circ}$

Composite Great Circle Sailing:

The great Circle track being always curved towards the nearest pole and the vertex being the closest to that pole, it happens that the track goes too high in latitude or crosses non-navigable waters due to icebergs, land and so on.

This is the moment ship-owners and navigation personnel decide to limit the extreme latitude to a more practical parallel.

We are presented with a situation where the initial track becomes a composite track with 3 tracks.

The first track is from the departure point to the point where the original track meets the parallel. That being said, the parallel representing the maximum latitude becomes a vertex for the first track and the third track where the parallel meets the track again. The second track is a regular rhumb line sailing, parallel sailing, on the parallel.

This gives us two right spherical triangles enabling us to compute the distances and the initial and final courses.

If $\varphi_{p}$ is the max latitude we can use the Napier’s formulas for the right spherical triangle.

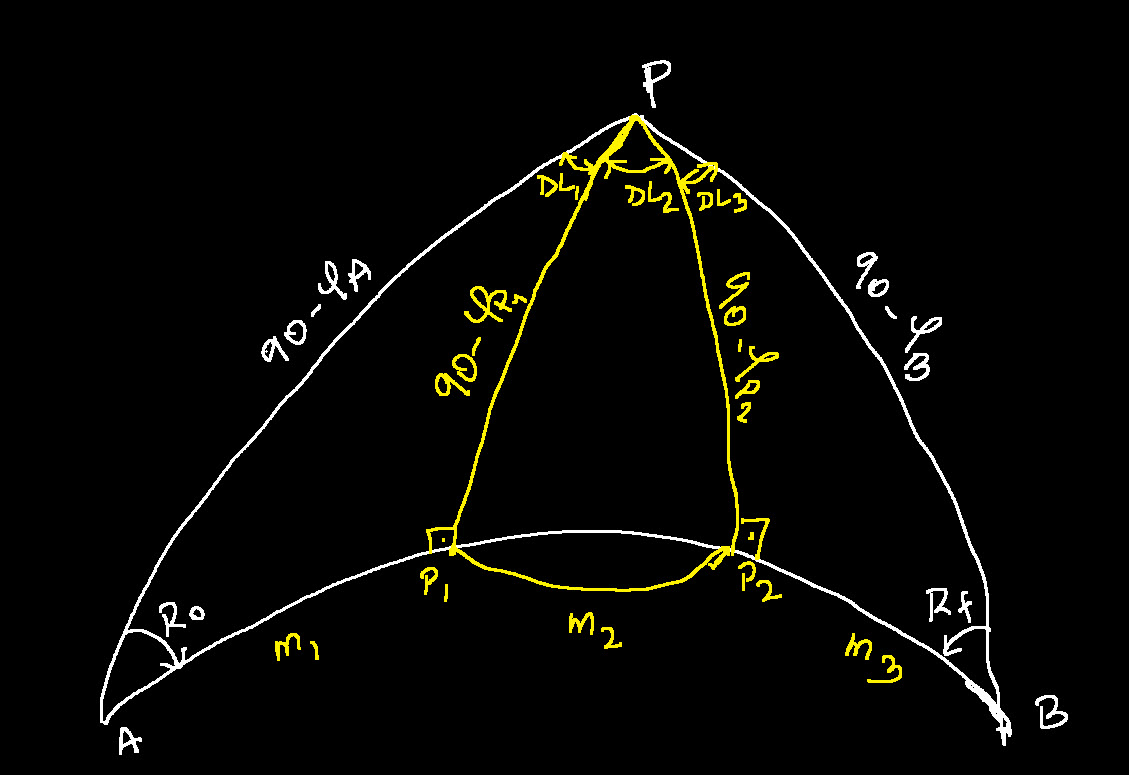
The initial and final courses:

$\displaystyle{\sin {R_0}}=\frac{\cos \varphi_{p}}{\cos \varphi_{A}}$

On the second triangle:

The final course is angle in $B$ added to or subtracted from $180^{\circ}$

$\displaystyle{\sin {R_f}}=\frac{\cos \varphi_{p}}{\cos \varphi_{B}}$

The difference in longitude can be calculated by:

For the first track:

$\displaystyle{\cos {DL_1}}=\frac{\tan {\varphi_{A}}}{\tan \varphi_{p}}$

For the third track:

$\displaystyle{\cos {DL_3}}=\frac{\tan {\varphi_{B}}}{\tan \varphi_{p}}$

Distance on first track:

$\displaystyle{\cos m_1}=\frac{\sin \varphi_{A}}{\sin \varphi_{p}}$

Distance on third track:

$\displaystyle{\cos m_3}=\frac{\sin \varphi_{B}}{\sin \varphi_{p}}$

Distance along the parallel:

$\displaystyle{m_2}=DL_p\cos {\varphi_{p}}$

Example:

A vessel is sailing on a great circle track between the two following points with a maximum latitude of $\varphi_{v}=45^{\circ}N$
Departure:
Latitude: $37^{\circ}48'N$
Longitude: $122^{\circ}40'W$

Destination:
Latitude: $35^{\circ}40'N$
Longitude: $141^{\circ}00'E$

Solution :
This is a composite sailing with three tracks

First track:

Initial Course:
$\sin {R_0}=\frac{\cos {\varphi_{p}}}{\cos {\varphi_{1}}}$
$\sin {R_0}=\frac{\cos {45}}{\cos {37^{\circ}48'}}$
$\sin {R_0}=0.89489628$
$R_0=N63.4951104W=296.5^{\circ}T$

The difference in Longitude (Departure) to the first intersection:
$\cos {DL_1}=\frac{\tan {\varphi_{1}}}{\tan {\varphi_{p}}}$
$\cos {DL_1}=\frac{\tan {37^{\circ}48'}}{\tan {45}}$
$\cos {DL_1}=0.775679511$
$DL_1=39^{\circ}8'W$ moving West.
Longitude of the First intersection:
$122^{\circ}40'W+39^{\circ}8'W=161^{\circ}48'W$

The first distance:
$\cos {m_1}=\frac{\sin {\varphi_{1}}}{\sin {\varphi_{p}}}$
$\cos {m_1}=\frac{\sin {37^{\circ}48'}}{\sin {45}}$
$\cos {m_1}=0.8667814678$
$m_1=1794.8$

The difference in Longitude (Departure) from the second intersection to the destination:
$\cos {DL_3}=\frac{\tan {\varphi_{2}}}{\tan {\varphi_{p}}}$
$\cos {DL_3}=\frac{\tan {35^{\circ}40'}}{\tan {45}}$
$\cos {DL_3}=0.7176910892$
$DL_1=44^{\circ}8.1'E$ East of Destination.
Longitude of the second intersection:
$141^{\circ}00'E+44^{\circ}8.1'E=185^{\circ}08.1'E$ We crossed the anti-meridian:

The Longitude is:
$360-185^{\circ}08.1'=174^{\circ}51.9'W$

The final distance:
$\cos {m_3}=\frac{\sin {\varphi_{2}}}{\sin {\varphi_{p}}}$
$\cos {m_3}=\frac{\sin {35^{\circ}40'}}{\sin {45}}$
$\cos {m_3}=0.824583609$
$m_3=2067.2$

The distance on the parallel track:
$DL_p=174^{\circ}51.9'W-161^{\circ}48'W=13^{\circ}03.9'=783.9$ Moving due West.
$m_2=DL_{p}\cos {\varphi_{p}}=783.9\cos {45}=554.3$

The total Distance:
$m=1794.8+554.3+2067.2=4416.3$

Practical Navigation

A ship’s officer is planning navigation between the following points:
From:
Latitude: $25^{\circ}41'N$
Longitude: $072^{\circ}10'W$

To:
Latitude: $33^{\circ}07'N$
Longitude: $017^{\circ}15'W$

He has to go through the following steps and needs your help:
1. Calculate the Rhumb Line course and distance (Mercator).
2. Calculate the total distance using great circle sailing
3. Calculate the initial course and final course on the great Circle track
4. Calculate the Latitude and longitude of the vertex on the great Circle track
5. Use waypoints about $5^{\circ}$ of longitude apart, find the coordinates, rhumb line distances and courses between consecutive waypoints.
6. Calculate the total distance of all waypoints and compare the three total distances found.

SOLUTION:
Rhumb Line Course and distance
We will use the following formulas:
$\tan {R_v}=\frac{G_2-G_1}{\lambda_2-\lambda_1}$
With:
$\lambda=\frac{180\times 60}{\pi}\ln {\tan {(45^{\circ}+\frac{\varphi}{2})}}$
The distance:
$m=\frac{\varphi_B-\varphi_A}{\cos {R_v}}$

The Difference in Longitude
$G_2-G_1=DG=017^{\circ}15'W-072^{\circ}10'W=54^{\circ}55'E$
In minutes of arc: $DG=60\times54+55=3295'$
$\lambda_1=\frac{180\times 60}{\pi}\ln {\tan {(45^{\circ}+\frac{\varphi_{1}}{2})}}$
$\lambda_1=\frac{180\times 60}{\pi}\ln {\tan {(45^{\circ}+\frac{25^{\circ}41'}{2})}}$
$\lambda_1=1595.361$
$\lambda_2=\frac{180\times 60}{\pi}\ln {\tan {(45^{\circ}+\frac{33^{\circ}07'}{2})}}$
$\lambda_2=2107.879$

$\tan {R_v}=\frac{DG}{\lambda_2-\lambda_1}$
$\tan {R_v}=\frac{3295}{2107.879-1595.361}$
$R_V=N81.2^{\circ}E= 081.2^{\circ}$

Distance:
$m=\frac{\varphi_B-\varphi_A}{\cos {R_v}}$
$m=60\times\frac{33^{\circ}07'-25^{\circ}41'}{\cos {81.15882305^{\circ}}}$
$m=2901.8\; Miles$
Mercator:
$R_o=081.2^{\circ}$
$Dist=2901.8\; Miles$

Great circle track:

$\cos {m}=\sin \varphi_{1} \sin \varphi_{2}+\cos \varphi_{1} \cos \varphi_{2}\cos {DG}$
$\cos {m}=\sin {25^{\circ}41'} \sin {33^{\circ}07'}+\cos {25^{\circ}41'} \cos {33^{\circ}07'}\cos {54^{\circ}55'}$
$\cos {m}=0.6706254694$
$m=47.8846428^{\circ}$

Distance
$m=2873.1$

Initial Course:
$\cos {R_0}=\frac{\sin {\varphi_{2}}-\sin {\varphi_{1}}\cos {m}}{\sin {m}\cos {\varphi_{1}}}$
$\cos {R_0}=\frac{\sin {33^{\circ}07'}-\sin {25^{\circ}41'}\cos {47.8846428^{\circ}}}{\sin {47.8846428^{\circ}}\cos {25^{\circ}41'}}$
$\cos {R_0}=0.382490874$
$R_0=67.51194128^{\circ}=N67.5^{\circ}E= 067.5^{\circ}$

Final Course:
$\cos {R_f}=\frac{\sin {\varphi_{1}}-\sin {\varphi_{2}}\cos {m}}{\sin {m}\cos {\varphi_{2}}}$
$\cos {R_f}=\frac{\sin {25^{\circ}41'}-\sin {33^{\circ}07'}\cos {47.8846428^{\circ}}}{\sin {47.8846428^{\circ}}\cos {33^{\circ}07'}}$
$\cos {R_f}=0.1078445412$
$R_f=S83.80892233^{\circ}E=096.2^{\circ}= 096.2^{\circ}$

Vertex Coordinates:
$\cos {\varphi_v}=|\sin {(R_0)}|\cos {(\varphi_1)}$
$\cos {DL_v}=\frac{\tan {(\varphi_1)}}{\tan {(\varphi_V)}}$

OR
$\cos {\varphi_v}=|\sin {(R_f)}|\cos {(\varphi_2)}$
$\cos {DL_v}=\frac{\tan {(\varphi_2)}}{\tan {(\varphi_V)}}$

Latitude of vertex:
$\cos {\varphi_v}=|\sin {(R_0)}|\cos {(\varphi_1)}$
$\cos {\varphi_v}=|\sin {(67.51194728^{\circ})}|\cos {(25^{\circ}41')}$
$\cos {\varphi_v}=0.8326750211$
$\varphi_v=33^{\circ}37.5'N$

Longitude of vertex:
$\cos {DL_v}=\frac{\tan {(\varphi_1)}}{\tan {(\varphi_V)}}$
$\cos {DL_v}=\frac{\tan {(25^{\circ}41')}}{\tan {(33^{\circ}37.5')}}$
$\cos {DL_v}=0.7231286694$
$DL_v=43.686603=43^{\circ}41.2'$ Moving East.
$L_v=072^{\circ}10'W+43^{\circ}41.2'E$
$L_v=028^{\circ}28.8'W$

Vertex:
$\varphi_v=33^{\circ}37.5'N$
$L_v=028^{\circ}28.8'W$

TABLE OF WAYPOINTS

Longitude	D Longitude to Vertex	Latitude	Course	Distance
$72^{\circ}10'W$	$43^{\circ}41.2'w$	$25^{\circ}41.0'N$	$069.1^{\circ}$	410.4
$65^{\circ}W$	$36^{\circ}31.2'w$	$28^{\circ}07.4'N$	$072.0^{\circ}$	276.4
$60^{\circ}W$	$31^{\circ}31.2'w$	$29^{\circ}33.0'N$	$074.4^{\circ}$	269.3
$55^{\circ}W$	$26^{\circ}31.2'w$	$30^{\circ}45.3'N$	$077.0^{\circ}$	263.2
$50^{\circ}W$	$21^{\circ}31.2'w$	$31^{\circ}44.7'N$	$079.6^{\circ}$	258.3
$45^{\circ}W$	$16^{\circ}31.2'w$	$32^{\circ}31.3'N$	$082.3^{\circ}$	254.5
$40^{\circ}W$	$11^{\circ}31.2'w$	$33^{\circ}05.4'N$	$085.0^{\circ}$	251.8
$35^{\circ}W$	$6^{\circ}31.2'w$	$33^{\circ}27.3'N$	$087.8^{\circ}$	250.3
$30^{\circ}W$	$1^{\circ}31.2'w$	$33^{\circ}37.0'N$	$090.5^{\circ}$	250.3
$25^{\circ}W$	$3^{\circ}28.8'e$	$33^{\circ}34.6'N$	$093.3^{\circ}$	250.7
$20^{\circ}W$	$8^{\circ}28.8'e$	$33^{\circ}20.1'N$	$095.4^{\circ}$	138.6
$17^{\circ}15'W$	$11^{\circ}13.8'e$	$33^{\circ}07.0'N$	ARRIVAL	ARRIVAL
				2873.8

Conclusion:

Using the waypoints we can see that we get the same distance as the great Circle track which is shorter than the Rhumb line (mercator) on a single track.

Post Views: 1,173

tv antenna from toptvantenna says:

April 10, 2023 at 10:03 am

Hi there, just became aware of your blog through Google, and found that it is truly informative.
I am gonna watch out for brussels. I’ll be grateful if you continue this in future.
Many people will be benefited from your writing. Cheers!

Navigation and Trigonometry

Navigation and Trigonometry

Rhumb Line Sailing: LOXODROMY

The Route:

The distance in nautical miles:

The route

Parallel sailing

Exercise 1:

Exercise 2:

Exercise 3

Great Circle Sailing: ORTHODROMY

Vertex Coordinates:

Composite Great Circle Sailing:

The initial and final courses:

Practical Navigation

TABLE OF WAYPOINTS

1 Comment

Leave a Reply Cancel reply