Selected Trigonometry Exercises – Page 3

Exercise 26:

Verify:
$\displaystyle{\tan {3x}}=\frac{\tan {x}(3-\tan^{2}x)}{1-3\tan^{2}x}$

Solution:

(1) $\begin{equation*} \begin{split} \displaystyle{\tan {3x}}&=\tan {(2x+x)}\\ &=\frac{\tan {2x}+\tan {x}}{1-\tan {2x}\tan {x}}\\ &=\frac{\frac{2\tan {x}}{1-\tan^{2}x+\tan {x}}}{1-\frac{2\tan {x}}{1-\tan^{2}x}\tan {x}}\\ &=\frac{2\tan {x}+ \tan {x}(1-\tan^{2}x)}{(1-\tan^{2}x)-2\tan {x}\tan{x}}\\ &=\frac{2\tan {x}+ \tan {x}(1-\tan^{2}x)}{(1-\tan^{2}x)-2\tan^{2}{x}}\\ &=\frac{3\tan {x}-\tan^{3}{x}}{1-3\tan^{2}x}\\ &=\frac{\tan {x}(3-\tan^{2}x)}{1-3\tan^{2}x} \end{split} \end{equation*}$

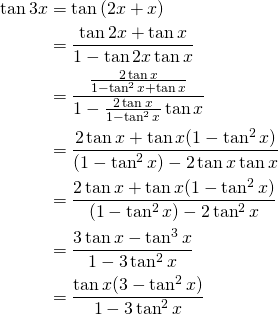
Finally:
$\displaystyle{\tan {3x}}=\frac{\tan {x}(3-\tan^{2}x)}{1-3\tan^{2}x}$

Exercise 27:

Solve for $\theta$ :
$\sin \theta-\sqrt{3}\cos \theta=\sqrt{3}$

Solution:

We have:
$\sin \theta-\sqrt{3}\sqrt{1-\sin^{2} \theta}=\sqrt{3}$

This yields:
$\sin \theta -\sqrt{3}=\sqrt{3}\sqrt{1-\sin^{2} \theta}$

Let’s square both side:
$(\sin \theta -\sqrt{3})^{2}=3(1-\sin^{2} \theta)$

$\sin^{2} \theta-2\sqrt{3}\sin \theta+3=3-3\sin^{2} \theta$
$\sin^{2} \theta+3\sin^{2} \theta-2\sqrt{3}\sin \theta=0$
$4\sin^{2} \theta-2\sqrt{3}\sin \theta=0$
$\sin {\theta}(4\sin \theta-2\sqrt{3})=0$

We have a couple of cases for base angles here:
$\sin \theta=0$
Looking at the figure, we see that the red lines are the values of the $cosine$ when the $sine$ is $0$
The angles here are:
$\theta_{1}=0^{\circ}$ and $\theta_{2}=180^{\circ}$
We have to exclude $0^{\circ}$ since it does not verify the equation.
However $180^{\circ}$ is a valid solution since $\cos 180^{\circ}=-1$

For the second factor:
$4\sin \theta-2\sqrt{3}=0\Rightarrow \sin \theta=\frac{\sqrt{3}}{2}$

From the figure we see two values:
The third angle is $60^{\circ}$
We can see that $\cos 60^{\circ}=\frac{1}{2}$
If we try to plug the values in the equation it is not a solution.

The fourth angle is $120^{\circ}$
We can see that $\cos 120^{\circ}=-\frac{\sqrt{3}}{2}$
This one verifies our equation.
So the angles are:
$120^{\circ}+k_{1}360^{\circ}$ and $180^{\circ}+k_{2}360^{\circ}$

Exercise 28:

Solve for $\theta$ :
$13\cot \theta+ 11 \csc \theta=6\sin \theta$

Solution:

We have:
$13\frac{\cos \theta}{\sin \theta}+\frac{11}{\sin \theta}=6 \sin \theta$

$13\cos \theta +11=6\sin^{2} \theta$

$13\cos \theta +11=6(1-\cos^{2} \theta)$
$6-6\cos^{2} \theta=13\cos \theta+11$

We get:
$6\cos^{2} \theta+13\cos \theta+11-6=0$
$6\cos^{2} \theta+13\cos \theta+5=0$

Let $\cos \theta=x$ with $-1 \leq x \leq 1$
We write:
$6x^{2}+13x+5=0$
$\Delta=169-4\times 6\times 5$
$\Delta=49$
$\sqrt{\Delta}=7$

The values of $x$ :
$x_{1}=\frac{-13+7}{12}=-\frac{1}{2}$

$x_{2}=\frac{-13-7}{12}=-\frac{20}{2}$
$x_{2}$ is not valid since it is less than $-1$

The possible values of $\theta$
Looking at the figure, for this $cosine$ we have two possible values for the $sine$

$\sin \theta_{1}=\frac{\sqrt{3}}{2}$
This yields:
$\theta_{1}=120^{\circ}$
Plug in:
$6\sin \theta_{1}=6 \times \frac{\sqrt{3}}{2}=3\sqrt{3}$

Now the left side:
$13 \frac{\frac{-1}{2}}{\frac{\sqrt{3}}{3}}+\frac{11}{\frac{3}{2}}=3\sqrt{3}$

The second angle is:
$\theta_{2}=240^{\circ}$
When we plug in this does verifies the equation.

The solutions:
$\theta_{1}=120^{\circ}+k_{1}360^{\circ}$
$\theta_{2}=240^{\circ}+k_{2}360^{\circ}$

Exercise 29:

Solve for $\theta$ :
$\sqrt{3}\sec \theta=2$

Solution:

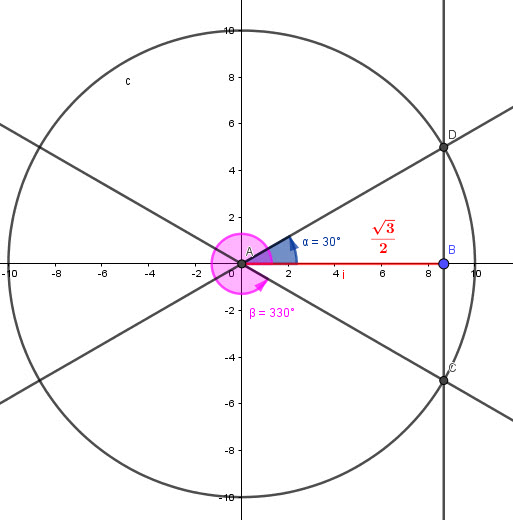
We can write:

$\sqrt{3}\cdot \frac{1}{\cos \theta}=2$

$2\cos \theta=\sqrt{3}$

$\cos \theta =\frac{\sqrt{3}}{2}\Leftarrow \theta=\frac{\pi}{6}$

The base angle here is $\frac{\pi}{6}$

Looking at the graph we have the folloing solutions:

$\theta=\frac{\pi}{6}+2K_{1}\pi$ and $\theta=\frac{11\pi}{6}+2K_{1}\pi$

Exercise 30:

Solve for $\theta$ :
$\sqrt{2}\csc x+5=3$

Solution:

$\sqrt{2}\csc x+5=3$

$\frac{\sqrt{2}}{\sin x}+5=3$

$\frac{\sqrt{2}}{\sin x}=-2$

$\sqrt{2}=-2\sin x$

$\sin x=-\frac{\sqrt{2}}{2}$

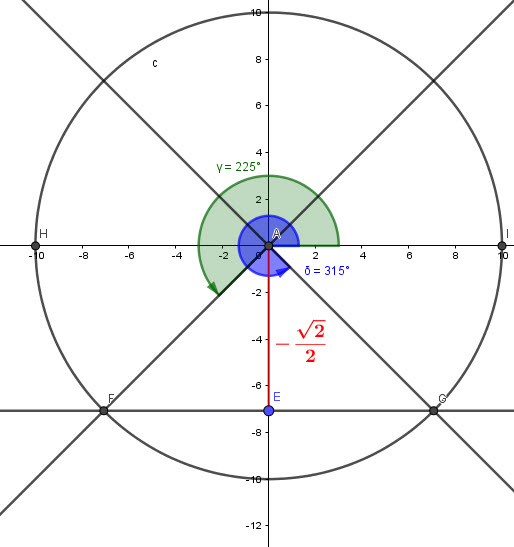
The base angle here is $\frac{\pi}{4}$

From the graph:

We can see that the two angles are:

$\pi+\frac{\pi}{4}=\frac{5\pi}{4}$

and

$2\pi-\frac{\pi}{4}=\frac{7\pi}{4}$

Finally the soultions are:

$\frac{5\pi}{4}+2k_{1}\pi$ and $\frac{7\pi}{4}+2k_{1}\pi$

Exercise 31:

Solve for $\theta$ :
$\cos 2\theta-3\sin \theta-2=0$

Solution:

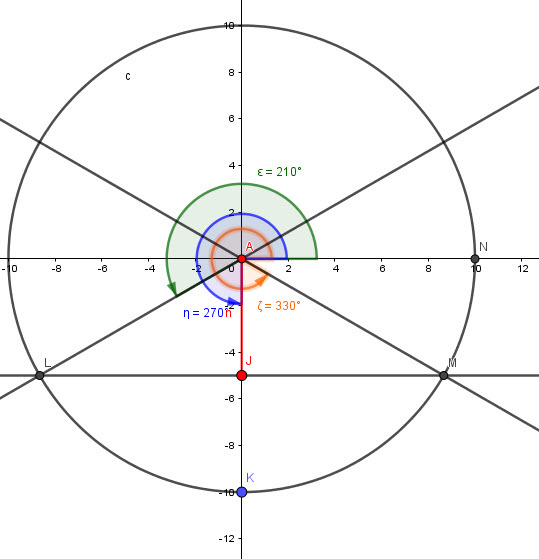
we know that:

$\cos 2\theta=1-2\sin^{2}\theta$

The equation becomes:

$1-2\sin^{2}\theta-3\sin \theta-2=0$

$-2\sin^{2}\theta-3\sin \theta-1=0$

We re-write:

$2\sin^{2}\theta+3\sin \theta+1=0$

let $\sin \theta=x$

$2x^{2}+3x+1=0$

$\Delta=9-8=0$

$x_{1}=\frac{-3+1}{4}=-\frac{1}{2}$

The base angle is $\frac{\pi}{6}$

From the graph:

$\theta_{1}=\pi+\frac{\pi}{6}=\frac{7\pi}{6}$

$\theta_{2}=2\pi-\frac{\pi}{6}=\frac{11\pi}{6}$

Both verify the equation.

The second case:

$x_{2}=\frac{-3-1}{4}=-1$

The base angle here is $\frac{3\pi}{2}$ and is the only one:

$\theta_{3}=\frac{3\pi}{2}$

This also satisfies the equation:

The solutions:

$\theta_{1}=\frac{7\pi}{6}$ , $\theta_{2}=\frac{3\pi}{2}$ and $\theta_{3}=\frac{11\pi}{6}$

Exercise 32:

Solve for $\theta$ :
$\sin \frac{\theta}{2}+ \cos \theta=0$

Solution:

But we know that:
$\cos \theta=1-2\sin^{2}\frac{\theta}{2}$

We get:
$\sin \frac{\theta}{2}+1-2\sin^{2}\frac{\theta}{2}=0$

$2\sin^{2}\frac{\theta}{2}-\sin \frac{\theta}{2}-1=0$

Let $\frac{\theta}{2}=x$

We write:
$2x^{2}-x-1=0$
$\Delta=1+8=9\Rightarrow \sqrt{\Delta}=3$
$x_{1}=\frac{1+3}{4}=1$
$x_{2}=\frac{1-3}{4}=\frac{-1}{2}$

Case 1:
$\sin \frac{\theta}{2}=1\Leftarrow \frac{\theta}{2}=\frac{\pi}{2}$
This gives:
$\theta_{1}=\pi$
This verifies the equation:
$1-1=0$

Case 2:

$\sin \frac{\theta}{2}=-\frac{1}{2}$

The base angle here is $\frac{\pi}{6}$
Two subsequent cases here:
$\frac{\theta}{2}=\pi+\frac{\pi}{6}=\frac{7\pi}{6}$
This yields:
$\theta_{2}=2\cdot \frac{7\pi}{6}=\frac{14\pi}{6}-2\pi=\frac{\pi}{3}$
This does not verify the equation and is not a solution:
$\frac{1}{2}+\frac{1}{2}\neq 0$

The second case here:
$\frac{\theta}{2}=2\pi-\frac{\pi}{6}=\frac{12\pi}{6}-\frac{\pi}{6}=\frac{11\pi}{6}$
$\theta_{3}=2\cdot\frac{11\pi}{6}-2\pi=\frac{10\pi}{6}=\frac{5\pi}{3}$
Checking in the equation:
$\frac{1}{2}+\frac{1}{2}\neq 0$

The solutions:
$\theta=\pi+2k\pi$

Exercise 33:

Solve for $\theta$ :
$\sin 3\theta \cos 2\theta+\cos 3\theta \sin 2\theta=1$

Solution:

$\sin 3\theta \cos 2\theta+\cos 3\theta \sin 2\theta=1$
$\sin (3\theta+2\theta)=1$
$\sin (5\theta)=1$

This gives:
$5\theta=\frac{\pi}{2}+2k\pi$
$\theta=\frac{\pi}{10}+\frac{2k\pi}{5}$

Exercise 34:

Solve for $\theta$ :
$2\cos^{2}{2\theta}+3\cos {2\theta}+1=0$

Solution:

$2\cos^{2}{2\theta}+3\cos {2\theta}+1=0$
Let $\cos {2\theta}=x$
We can write:
$2x^{2}+3x+1=0$
$\Delta=9-8=1\Rightarrow \sqrt{\Delta}=1$

Two roots here:
$x_{1}=\frac{-3+1}{4}=-\frac{1}{2}$

This root leads to two solutions:
$\cos {2\theta}=-\frac{1}{2}$ :

Case 1:
$2\theta=\pi-\frac{\pi}{3}=\frac{2\pi}{3}$
$2\theta_{1}=\frac{2\pi}{3}+2k\pi \Rightarrow \theta_{1}=\frac{\pi}{3}+k\pi$

Case 2:
$2\theta=\pi+\frac{\pi}{3}=\frac{4\pi}{3}$
$2\theta_{1}=\frac{4\pi}{3}+2k\pi \Rightarrow \theta_{1}=\frac{2\pi}{3}+k\pi$

Both cases verify the equation:
$2\times (-\frac{1}{2})^{2}+3\times(\frac{-1}{2})+1=2\times \frac{2}{4}-\frac{3}{2}+1=0$

For the second root:

$x_{2}=-1$
One solution here:
$\cos {2\theta}=-1\Leftarrow 2\theta=\pi+ 2k\pi$
The solution:
$2\theta=\pi+2k\pi\Rightarrow \theta=\frac{\pi}{2}+k\pi$
This verifies the equation:
$2(1)+3(-1)+1=2-3+1=0$

Finally the solutions are:
$\frac{\pi}{3}+k_{1}\pi$ , $\frac{\pi}{2}+k_{2}\pi$ and $\frac{2\pi}{3}+k_{3}\pi$

Exercise 35:

Solve for $\theta$ :
$\sin^{2}{4\theta}=0$

Solution:

[accordion hideSpeed=”300″ showSpeed=”400″]

[item title=”Click here to see the solution to ex35 “]

$\sin^{2}{4\theta}=0$

Let $\sin {4\theta}=x$

We get:
$x^{2}=1$

Roots:

$x_{1}=1$
This means:
$\sin {4\theta}=1\Leftarrow 4\theta=\frac{\pi}{2}+2k\pi$
This yields:
$\theta_{1}=\frac{\pi}{8}+\frac{k\pi}{2}$

$x_{1}=-1$
$\sin {4\theta}=-1\Leftarrow 4\theta=\frac{3\pi}{2}+2k\pi$
This yields:
$\theta_{2}=\frac{3\pi}{8}+\frac{k\pi}{2}$

Finally:
The solutions are:
$\frac{\pi}{8}+\frac{k\pi}{2}$ and $\frac{3\pi}{8}+\frac{k\pi}{2}$

Exercise 36:

Solve for $\theta$ :
$\sin 2\theta-\sin \theta=0$

Solution:

$\sin 2\theta-\sin \theta=0$
We write:
$2\sin \theta \cos \theta-\sin \theta=0$
$\sin {\theta}(2\cos \theta-1)=0$

Two cases:
$\sin \theta=0$
This has two subsequent possibilities:
$\theta_{1}=0+2k_{1}\pi$
and
$\theta_{2}=\pi+2k_{2}\pi$

Both verify the equation.

The other case:

$2\cos {\theta}-1=0$
$\cos {\theta}=\frac{1}{2}$
Two subsequent solutions:
$\theta_{3}=\frac{\pi}{3}+2k_{3}\pi$
and
$\theta_{4}=2\pi-\frac{\pi}{3}+2k_{4}\pi=\frac{5\pi}{3}+2k_{4}\pi$

For $\theta_{1}$ :
$\sin {2\times 0}-\sin {0}=0$
means $0-0=0$ which is true.

For $\theta_{2}$ :
$\sin {2\times \pi}-\sin {\pi}=0$
means $0-0=0$ which is true.

For $\theta_{3}$ :
$\sin {(2\times \frac{\pi}{3})}-\sin {\frac{\pi}{3}}=0$
means $\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}=0$ which is true.

For $\theta_{4}$ :
$\sin {(2\times \frac{5\pi}{3})}-\sin {\frac{5\pi}{3}}=0$
$\sin {\frac{4\pi}{3}}-\sin {\frac{5\pi}{3}}=0$
$-\frac{\sqrt{3}}{2}-\frac{(-\sqrt{3})}{2}=0$ which is true.

Finally the solutions are:

$0+2k_{1}\pi$ , $\pi+2k_{2}\pi$ , $\frac{\pi}{3}+2k_{3}\pi$ and $\frac{5\pi}{3}+2k_{4}\pi$

Exercise 37:

Solve for $\theta$ :
$2\cos ^{2} {2\theta}-3\cos {2\theta}=-1$

Solution:

$2\cos ^{2} {2\theta}-3\cos {2\theta}=-1$

Let $\cos {2\theta}=x$

This yields:

$2x^{2}-3x+1=0$

$\Delta=9-8=1$

$\sqrt{\Delta}=1$

$x_{1}=\frac{3+1}{4}=1$

$x_{2}=\frac{3-1}{4}=\frac{1}{2}$

Case 1:

$\cos {2\theta}=1 \Leftarrow 2\theta=0+2k_{1}\pi$

This gives:

$\theta_{1}=0+k_{1}\pi$

Case 2:

$\cos {2\theta}=\frac{1}{2}$

Looking at the graph, we have two additional cases:

$2\theta_{2}=\frac{\pi}{3}+2k_{2}\pi$

$\theta_{2}=\frac{\pi}{6}+k_{2}\pi$

The other additional case:

$2\theta_{3}=\frac{5\pi}{3}+2k_{3}\pi$

$\theta_{3}=\frac{5\pi}{6}+k_{3}\pi$

Finally the solutions are:

$0+k_{1}\pi$ , $\frac{\pi}{6}+k_{2}\pi$ , $\frac{5\pi}{6}+k_{3}\pi$

Exercise 38:

Given $A=30^{\circ}$ , $b=12$ and $a=6$

Find $B$ , $C$ and $c$

Solution:

Since $b=2a$ , we have the angle $B=90^{\circ}$

That means $C=60^{\circ}$

For side $c$

$\frac{c}{\sin C}=\frac{a}{\sin A}$

$c=\frac{6\sin 60}{\sin 30}$

$c=6\sqrt{3}$

$c=10.39$

Exercise 39:

Given $A=43^{\circ}$ , $b=37$ and $a=31$

Find $B$ , $C$ and $c$

Solution:

We can see that we two possible values for $c$ :

$a^{2}=b^{2}+c^{2}-2bc\cos A$

This yields:

$c^{2}-(2b\cos A)c+b^{2}-a^{2}=0$

$c^{2}-(2\times 37 \times \cos 43)c+37^{2}-31^{2}$

$c^{2}-54.12017c+408=0$

$\Delta=(-54.12017)^2-4\times 1\times 408=1296.992801$

$\sqrt{\Delta}=36.014$

$c_{1}=\frac{54.12017+36.014}{2}=45.067$

$c_{2}=\frac{54.12017-36.014}{2}=9.053$

For $c_{1}$

$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{31^{2}+45.067^{2}-37^{2}}{2\times31 \times 45.067}$

$\cos B=0.580868$

$B=54.5^{\circ}$

That means:

$C=180-(43+54.5)=82.5^{\circ}$

$C=82.5^{\circ}$

For $c_{2}$

$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{31^{2}+9.053^{2}-37^{2}}{2\times31 \times 9.053}$

$\cos B=-0.580886$

$B=125.5^{\circ}$

That means:

$C=180-(43+125.5)=11.5^{\circ}$

$C=11.5^{\circ}$

[/item] [/accordion]

Exercise 40:

Given $a=832$ , $b=623$ and $c=345$
Find Angles $A$ , $B$ and $C$

Solution:

[accordion hideSpeed=”300″ showSpeed=”400″]

[item title=”Click here to see the solution to ex40 “]

Looking at the sides we can deduct that the biggest angle is $A$

Let’s calculate it:

$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}$
$\cos A=\frac{623^{2}+345^{2}-832^{2}}{2\times 623 \times 345}$
$\cos A=-0.4305255$

$m\angle A=115.5^{\circ}$
No other angle is obtuse.

$\frac{\sin A}{a}=\frac{\sin B}{b}$
$\sin B=\frac{b \sin A}{a}=\frac{623\times \sin 115.5}{832}$

$\sin B=0.675854$
$m\angle B=42.5^{\circ}$

The angle $C$ :
$m\angle C=180-(115.5+42.5)=180-158=22^{\circ}$

Finally:
$m\angle A=115.5^{\circ}$ , $m\angle B=42.5^{\circ}$ and $m\angle C=22^{\circ}$

Exercise 41:

Given $a=48$ , $b=75$ and $c=63$
Find Angles $A$ , $B$ and $C$

Solution:

Looking at the sides we can deduct that the biggest angle is $B$

Let’s calculate it:

$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}$
$\cos B=\frac{48^{2}+63^{2}-75^{2}}{2\times 48 \times 63}$
$\cos B=-0.1071429$

$m\angle B=83.9^{\circ}$
No other angle is obtuse.

$\frac{\sin C}{c}=\frac{\sin B}{b}$
$\sin C=\frac{c \sin B}{b}=\frac{63\times \sin 83.85}{75}$

$\sin C=0.8351656594$
$m\angle C=56.6^{\circ}$

The angle $A$ :
$m\angle A=180-(83.9+56.6)=180-140.5=39.5^{\circ}$

Finally:
$m\angle A=39.5^{\circ}$ , $m\angle B=83.9^{\circ}$ and $m\angle C=56.6^{\circ}$

Exercise 42:

Given $C=51.5^{\circ}$ , $c=707$ and $b=821$
Find $A$ , $B$ and $a$

Solution:

We know that:
$c^{2}=a^{2}+b^{2}-2ab\cos C$
We get
$a^{2}-(2b\cos C)a+b^{2}-c^{2}=0$
$a^{2}-(2\times 821\times \cos 51.5)a+821^{2}-707^{2}$
$a^{2}-1022.169a+174192=0$

We solve for $a$ :
$\Delta=(-1022.169)^{2}-4\times 1\times 174192=348061.4646$
$\sqrt{\Delta}=589.967$
$a_{1}=\frac{1022.169+589.967}{2}=806$

The angles:
$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}$

$\cos A=\frac{821^{2}+707^{2}-806^{2}}{2\times 821 \times 707}$

$\cos A=0.451595$
$m\angle A=63.2^{\circ}$
$m\angle B=180-(63.2+51.5)=180-114.7=65.3$

Case summary:
$m\angle A=63.2^{\circ}$ , $m\angle B=65.3^{\circ}$ and $a=806$

$a_{2}=\frac{1022.169-589.967}{2}=216$

The angles:
$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}$

$\cos A=\frac{821^{2}+707^{2}-216^{2}}{2\times 821 \times 707}$

$\cos A=0.9710051$
$m\angle A=13.8^{\circ}$
$m\angle B=180-(13.8+51.5)=180-65.3=114.7$

Case summary:
$m\angle A=13.8^{\circ}$ , $m\angle B=114.7^{\circ}$ and $a=216$

Exercise 43:

Simplify:

$\displaystyle{\frac{\sin {\frac{\theta}{2}}}{\csc {\frac{\theta}{2}}}+\frac{\cos {\frac{\theta}{2}}}{\sec {\frac{\theta}{2}}}}$

Solution:

$\displaystyle{\frac{\sin {\frac{\theta}{2}}}{\csc {\frac{\theta}{2}}}+\frac{\cos {\frac{\theta}{2}}}{\sec {\frac{\theta}{2}}}}=\sin {\frac{x}{2}}\times \sin {\frac{x}{2}}+\cos {\frac{x}{2}}\times \cos {\frac{x}{2}}=\sin^{2} {\frac{x}{2}}+\cos^{2} {\frac{x}{2}}=1$

Finally:

$\displaystyle{\frac{\sin {\frac{\theta}{2}}}{\csc {\frac{\theta}{2}}}+\frac{\cos {\frac{\theta}{2}}}{\sec {\frac{\theta}{2}}}}=1$

Exercise 44:

Simplify:

$(1-sin^{2}\theta)(1+\tan^{2}\theta)$

Solution:

$(1-sin^{2}\theta)(1+\tan^{2}\theta)=\cos^{2}{\theta}(1+\frac{\sin^{2}\theta}{\cos^{2}\theta}=\cos^{2}{\theta}(\frac{\cos^{2}{\theta}+\sin^{2}{\theta}}{\cos^{2}{\theta}})=1$

Exercise 45:

Verify that:

$\sin(\theta+\pi)=-\sin \theta$

Solution:

$\sin(\theta+\pi)=\sin \theta \cos \pi+ \cos \theta \sin \pi=-\sin \theta+0=-\sin \theta$

$\sin(\theta+\pi)=-\sin \theta$

Finally:

$\sin(\theta+\pi)=-\sin \theta$

Exercise 46:

Evaluate:

$\sin(\theta+\frac{\pi}{4})$

Solution:

$\sin(\theta+\frac{\pi}{4})=\sin \theta \cos \frac{\pi}{4}+\cos \theta \sin \frac{\pi}{4}=\frac{\sqrt{2}}{2}(\sin \theta+ \cos \theta)$

Finally

$\sin(\theta+\frac{\pi}{4})=\frac{\sqrt{2}}{2}(\sin \theta+ \cos \theta)$

Exercise 47:

Evaluate:

$2-\cos^{2}\theta=4\sin^{2}\frac{\theta}{2}$

Solution:

$2-\cos^{2}\theta=4\sin^{2}\frac{\theta}{2}$

$2-\cos^{2}\theta-4\sin^{2}\frac{\theta}{2}=0$

$2(1-2\sin^{2}\frac{\theta}{2})-\cos^{2}\theta=0$

$2\cos \theta--\cos^{2}\theta=0$

$\cos {\theta} (2-\cos \theta)=0$

Only the first factor:

$\cos \theta=0$

Two cases:

$\theta_{1}=\frac{\pi}{2}+2k_{1}\pi$

$\theta_{2}=\frac{3\pi}{2}+2k_{2}\pi$

Exercise 48:

Solve for $\theta$

$4\sin^{2}{\theta}\tan {\theta}-\tan {\theta}=0$

Solution:

$4\sin^{2}{\theta}\tan {\theta}-\tan {\theta}=0$

We factor:
$\tan {\theta}(4\sin^{2}{\theta}-1)=0$

We have to check both factors:

First factor:
$\tan {\theta}=0$
$\theta_{1}=0+2k_{1}\pi$ with $k_{1} \in \mathbb{Z}$

$\theta_{2}=\pi+2k_{2}\pi$ with $k_{2}\in \mathbb{Z}$

Second Factor:
$4\sin^{2}{\theta}-1=0$
$4\sin^{2}{\theta}=1$
$\sin^{2}{\theta}=\frac{1}{4}$

Case when $\sin {\theta}=\frac{1}{2}$
Base angle here is $\frac{\pi}{6}$

$\theta_{3}=\frac{\pi}{6}+2k_{3}\pi$ with $k_{3}\in \mathbb{Z}$

$\theta_{4}=\pi-\frac{\pi}{6}+2k_{4}\pi=\frac{5\pi}{6}+2k_{4}\pi$ with $k_{4}\in \mathbb{Z}$

Case when $\sin {\theta}=-\frac{1}{2}$
Base angle here is $\frac{\pi}{6}$

$\theta_{5}=\pi+\frac{\pi}{6}+2k_{5}\pi=\frac{7\pi}{6}+2k_{5}\pi$ with $k_{5}\in \mathbb{Z}$

$\theta_{6}=2\pi-\frac{\pi}{6}+2k_{6}\pi=\frac{11\pi}{6}+2k_{6}\pi$ with $k_{6}\in \mathbb{Z}$

Finally all 6 solutions verify the equation:

$\theta_{1}=0+2k_{1}\pi$ with $k_{1}\in \mathbb{Z}$

$\theta_{2}=\pi+2k_{2}\pi$ with $k_{2}\in \mathbb{Z}$
$\theta_{3}=\frac{\pi}{6}+2k_{3}\pi$ with $k_{3}\in \mathbb{Z}$

$\theta_{4}=\pi-\frac{\pi}{6}+2k_{4}\pi=\frac{5\pi}{6}+2k_{4}\pi$ with $k_{4}\in \mathbb{Z}$
$\theta_{5}=\pi+\frac{\pi}{6}+2k_{5}\pi=\frac{7\pi}{6}+2k_{5}\pi$ with $k_{5}\in \mathbb{Z}$

$\theta_{6}=2\pi-\frac{\pi}{6}+2k_{6}\pi=\frac{11\pi}{6}+2k_{6}\pi$ with $k_{6}\in \mathbb{Z}$