
In the following example, professor Alfred explains how we can save time by using the “poet’s” way, an elegant method, instead of what we call “Peasant’s” method.
Most of us hurry up when faced with a problem to solve. While we may eventually find a solution, it is always useful to make sure that there is no other shorter way to solve the problem before we dive into heavy calculations.
To better understand this difference, let’s consider the following problem:
“The sum of two numbers is 2. The product of the same two numbers is 3.
Find the sum of the reciprocals of these two numbers”
We can see that this problem does not ask us to find the 2 numbers.
The “Peasant’s way”
Let ![]() and
and ![]() be the 2 numbers.
be the 2 numbers.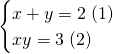
From (1) we have: ![]()
In 2 by substitution:![]() (3)
(3)![]()
![]()
![]()
There are no real roots but let’s ramp it up to the complex number sysem:![]()
![]()
![]()
The same way we find:![]()
From (3):
Let’s use ![]()
![]()
This is the ![]() of the complex
of the complex ![]()
We verify:
Sum:![]()
The imaginary parts cancel out:![]()
The product:
![]()
Now let’s answer the question, the sum of the reciprocals:
![]()
![]()
The answer
We have wasted time calculating the 2 numbers and we were even pushed to use the complex number system to solve a small problem that did not need all this effort. We could even have made mistakes.
The “poet’s” way:
Rarely used way but efficient, short and time saving.
From the prompt we can pull: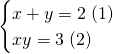
Final prompt item:![]() is to be found.
is to be found.
But:![]()
But from 1 ans 2:
We can plug in:![]()
We did not need any advanced concept to solve this.
Conclusion:
I expect students to use the concepts of this article every time they have to solve a problem. There maybe a huge tme saving approach hidden into some prompts.
Happy solving.


Be the first to comment