Calculs d’Intégrale

Après avoir parcouru les techniques d’intégration, nous sommes prêts à utiliser les primitives dans des calculs pratiques.

L’intégrale défini s’utilise dans les calculs d’aires, de longueurs, de volumes et d’autres calculs qui ne peuvent s’effectuer par voie normale.

Nous supposons que les Sommes de Riemann ont été vues dans les classes et on passe directement aux calculs d’intégrales.

Définition Rapide: Somme de Rienman

Si une fonction $f(x)$ est définie dans l’intervalle $[a,b]$ .

Définition:

Soit $f(x)$ définie dans l’intervalle fermé $[a,b]$ et $\Delta$ une division de $[a,b]$

noté:

$a=x_{0}<x_{1}<x_{2}<x_{3}< \cdots <x_{n-1}<x_{n}=b$

Quand $\Delta x_{i}$ est la $ième$ subdivision.

Si $c_{i}$ est un point de la $ième$ subdivision, alors la somme:

$\sum_{i=1}^{n} f(c_{i}) \Delta x_{i}$

, $x_{i-1} \leq c_{i} \leq x_{i}$

C’est la Somme de Riemann de $f$ pour la subdivision $\Delta$

Revenons au su.

Sir Isaac Newton et Gottfried Wilhelm Leibniz avaient trouver un chemin facile pour l’évaluation des intégrales.

Si $F$ est une primitive continue sur $f$ dans l’intervalle $[a,b]$ , on peut écrire:

$\int_a^b f(x) \;dx= F(b)-F(a)$

C’est aussi noté:

$\int_a^b f(x) \;dx= [F(x)]_a^b$

Théorème Fondamental du calcul intégral:

Si $a \leq x \leq b$ , et $F(x)$ est une primitive $f(x)$ :

$\int_a^b f(x) \;dx= F(x)\Big |_a^b=F(b)- F(a)$

Nous avons les propriétés suivantes:

$\int_a^b c \;dx= c(b-a)$

Exemple:

$\int_3^8 3 \;dx= 3(8-3)=15$

C’est l’aire sous la courbe $y=3$ . Ici la courbe est une droite

Nous aurons aussi les propriétés suivantes:

$\int_a^b cf(x) \;dx= c\int_a^b f(x) \;dx$

Union d’Intervalles:

Si $a< c < b$ on peut écrire:

$\int_a^b f(x) \;dx= \int_a^c f(x) \;dx +\int_c^b f(x) \;dx$

Théorème de la valeur moyenne:

La valeur moyenne d’une fonction $f$ ayant une primitive sur $[a,b]$ la valeur moyenne de $f(x)$ est:

$\overline{y}=\frac{1}{b-a}\int_a^b f(x) \;dx$

Aires d’intégration:

Les aires d’intégration peuvent se définir comme aires entre deux courbes. S’il n’y a pas une deuxième courbe, la seconde fonction est simplement la droite $f(x)=0$ . On est dans le cas des aires sous la courbe.

Pour une courbe avec des aires positives et négative, de part et d’autre de l’axe des $x$ , nous devons soustraire l’aire négative pour la rendre positive.

Exemple:
Nous avons deux fonctions dont laire se trouve entre les deux point d’intersection:

$f(x)=-x^{2}+6$

$g(x)=x$

On peut simplement écrire:

(1) $\begin{equation*} \begin{split} \displaystyle {\int \limits_{-3}^{2} (-x^{2}+6-x)\;dx}&= -\frac{x^{3}}{3}+6x-\frac{x^{2}}{2}\Big |_{-3}^{2}\\ &=-\frac{2^{3}}{3}+6(2)-\frac{2^{2}}{2}-(-\frac{-3^{3}}{3}+6(-3)-\frac{-3^{2}}{2} \\ &=-\frac{8}{3}+12-\frac{4}{2}-(\frac{27}{3}+6(-3)-\frac{9}{2})\\ &=\frac{-16}{6}+\frac{114}{6}+\frac{27}{6}=\frac{125}{6} \end{split} \end{equation*}$

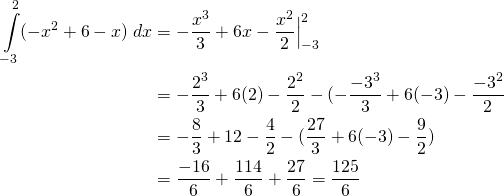
Longeur d’une courbe:

Nous savons comment calculer la distance entre deux points $M(x_1,y_1)$ et $N(x_2,y_2)$ qui s’écrit:

$MN=\sqrt{(x_2-x_1)^{2}+ (y_2-y_1)^{2} }$

Si nous avons une courbe et nous voulons connaître la longueur entre deux points $A$ et $B$ , on peut utiliser la somme de deux cordes courtes comme la corde $MN$ .

Plus ces cordes deviennent petites, plus on se rapproche de la longueur réelle.

Si nous appelons $\delta x$ et $\delta y$ les variations de $x$ et de $y$ , la longueur de chaque petit segment peut se calculer par la formule de calcul de distances.

$MN=\sqrt{(\delta x)^{2}+ (\delta y)^{2} }$

Quand $M$ et $N$ se rapprochent infiniment de sorte que $\delta x$ tend vers $0$ , $\delta x \rightarrow 0$ , On peut écrire: Avec $S=AB$

$MN=\sqrt{(dx)^{2}+ (dy)^{2} }$

$S=\int_a^b \sqrt{1+ (\frac{dy}{dx})^{2} } \cdot dx$

Finalement, la longueur de l’arc se note:

$S=\int_a^b \sqrt{1+ (\frac{dy}{dx})^{2} } \cdot dx$

Exemple:
Soit le cercle $x^{2}+y^{2}=r^{2}$
Trouver les formules de l’aire et de la circonférence en utilisant le calcul intégral.

Solution:

$x^{2}+y^{2}=r^{2}$

$y^{2}-r^{2}-x^{2}$

Dérivation implicite:

$2y \frac{dy}{dx}=0-2x$

$2y \frac{dy}{dx}=-2x$

$\frac{dy}{dx}=-\frac{2x}{2y}$

$\frac{dy}{dx}=-\frac{x}{y}$

Mais:
$y=\sqrt{ r^{2}-x^{2}}$

Nous avons:

$\frac{dy}{dx}=\frac{-x}{\sqrt{ r^{2}-x^{2}}}$

$(\frac{dy}{dx})^{2}=\frac{x^{2}}{r^{2}-x^{2}}$

Pour l’aire:
Prenons le premier quadrant:

$A_{1}=\int_0^r \sqrt{r^{2}-x^{2}}\; dx$

Soit $x=r \sin \theta$

$dx= r \cos \theta ; d \theta$

Nous aurons alors $\sin \theta=\frac{x}{r}$

Pour $x=0$

$\sin \theta=0 \Leftarrow \theta=0$

For $x=r$

$\sin \theta=\frac{r}{r}=1 \Leftarrow \theta=\frac{\pi}{2}$

Alors l’aire est:

$A_{1}=\int_{0}^{\frac{\pi}{2}} \sqrt{r^{2}-r^{2} \sin^{2} \theta} \cdot r \cos \theta \; d \theta$

$A_{1}=r\int_{0}^{\frac{\pi}{2}} \sqrt{1- \sin^{2} \theta} \cdot r \cos \theta \; d \theta$

$A_{1}=r^{2}\int_{0}^{\frac{\pi}{2}} \sqrt{ \cos^{2} \theta} \cdot \cos \theta \; d \theta$

$A_{1}=r^{2} \int_{0}^{\frac{\pi}{2}} \cos \theta \cdot \cos \theta \; d \theta$

$A_{1}=r^{2}\int_{0}^{\frac{\pi}{2}} \cos ^{2} \theta \; d \theta$

$A_{1}=r^{2}\int_{0}^{\frac{\pi}{2}} \frac{\cos 2\theta +1} {2} \; d \theta$

$A_{1}=\frac{r^{2}}{2}\int_{0}^{\frac{\pi}{2}} \cos 2\theta \; d \theta+ \frac{r^{2}}{2}\int_{0}^{\frac{\pi}{2}} d \theta$

$A_{1}=\frac{r^{2}}{2}\cdot \frac{1}{2} \sin 2\theta |_{0}^{\frac{\pi}{2}}+ \frac{r^{2}}{2} \cdot \frac{1}{2}\theta |_{0}^{\frac{\pi}{2}}$

$A_{1}=0-0+\frac{\pi r^{2}}{4}-0$

$A_{1}=\frac{\pi r^{2}}{4}$

Et comme nous 4 quadrants

$A=4A_{1}=\frac{\pi r^{2}}{4}$

$A=\pi r^{2}$

Finalement l’aire du cercle:

$A=\pi r^{2}$

Pour la circomference:

La même technique va s’imposer:

$S_{1}= \int_{0}^{r} \sqrt{1+ (\frac{dy}{dx})^{2}} \;dx$

$S_{1}= \int_{0}^{r} \sqrt{1+ \frac{x^{2}}{r^{2}-x^{2}}} \; dx$

$S_{1}= \int_{0}^{r} \sqrt{ \frac{r^{2}-x^{2}+x^{2}}{r^{2}-x^{2}}} \; dx$

$S_{1}= \int_{0}^{r} \sqrt{ \frac{r^{2}}{r^{2}-x^{2}}} \; dx$

$S_{1}= r\int_{0}^{r} \sqrt{ \frac{1}{r^{2}-x^{2}}} \; dx$

$S_{1}= r \int_{0}^{r} \frac{dx}{\sqrt{r^{2}-x^{2}}}$

$S_{1}= r \sin^{-1} \frac{x}{r} |_{0}^{1}$

$S_{1}= r [\sin^{-1} (1)]- [\sin^{-1} (0)]$

$S_{1}= r \frac{\pi}{2}-0$

$S_{1}= \frac{r}{2} \pi$

Pour les 4 quadrants:

La circonference sera:

$S= 4\frac{r}{2} \pi$

$S= 2 \pi r$

Finally:
La circonference est de:

$S= 2 \pi r$

Théorème de Charles

Si nous calculons l’aire totale, on utilise la méthode suivante:

Aire Nette=Aire positive (au dessus de $x$ -Aire négative, en dessous de $x$

Si l’intégrale est définie dans l’intervalle $[a,b]$ de sorte que l’on a une aire $A_{1}$ au dessus de $x-axis$ et $A_{2}$ en dessous de $x-axis$ , l’aire calculée est de:

$\int_{a}^{b} f(x)\;dx=A_{1}-A_{2}$

Exemple: Trouver l’aire entre la courbe de $f(x)=3x$ et l’axe des $x$ sur $[-2,2]$

On calcule comme suit:

$\int_{-2}^{2}3x\;dx=6-6=0$

Aire Totale:

Si l’intégrale est définie sur l’intervalle $[a,b]$ et nous avons 2 aires $A_{1}$ qui est au dessus et $A_{2}$ qui est en dessous de $x$ , laire nette est de:

$\int_{a}^{b} f(x)\;dx=A_{1}+A_{2}$

Il faut toujours examiner la courbe.

Aires entre Courbes:

Si $f(x)$ et $g(x)$ sont deux fonctions continues sur $[a,b]$ et $f(x) \geq g(x)$ , l’aire entre les deux courbes est:

$A=\int_{a}^{b}[f(x)-g(x)]\; dx$

Exemple:

Trouver l’aire entre les deux courbes qui suivent dans l’intervalle $[1,3]$

$f(x)=2x+3$

$g(x)=-x+4$

Le graphe de $f(x) \geq g(x)$ sur l’intervalle:

$a= \int_{1}^{3}[f(x)-g(x)]\; dx= \int_{1}^{3}[(2x+3)-(-x+4)]\; dx=\int_{1}^{3}3x-1\; dx$

$\int_{1}^{3}3x-1\; dx=\int_{1}^{3}3x-\int_{1}^{3}dx=3\frac{x^{2}}{2}|_{1}^{3}-x|_{1}^{3}=\frac{3 \times 9}{2}-\frac{3 \times 1}{2}-3(1)+1(1)=12-3+1=10$

Quand c’est une aire délimitée, nous devrons d’abord calculer les points d’intersection des deux courbes.

Aire composée entre deux courbes:

Lorsque les courbes se coupent en de multiples points, il sera nécessaire d’examiner les courbes et calculer les intégrales en tant que valeurs absolues de l’aire.
$Area=\int_{a}^{b}|f(x)-g(x)|\;dx$

Régions complexes:

L’aire suivante est délimitée par la fonction $f(x)=\sqrt(x)$ et $g(x)=-x+5$

On divise l’intégrale au niveau du point d’intersection.

Solides de revolution et Surface des aires

Si f(x) est une fonction positive sur l’intervalle $[a,b]$ .

Alors, la surface de l’aire de la surfacede revolution formée par la rotation du graphe de $f(x)$ autour de l’axe des $xs$ est donnée par:

$SA=\int_{a}^{b}(2 \pi f(x) \sqrt{1+(f'(x))^{2}}) \;dx$

Si nous prenons $g(y)$ et faisons tourner autour de l’axe des $y$

$SA=\int_{a}^{b}(2 \pi g(y) \sqrt{1+(g'(y))^{2}}) \;dy$

Exemple:

La droite $f(x)=r$ est tournée autour de l’axe des $x$ sur l’intervalle $[a,b]$
Trouver l’aire de la surface de Revolution:

$SA=\int_{a}^{b}(2 \pi f(x) \sqrt{1+(f'(x))^{2}}) \;dx$

Dans cette situation $f'(x)=0$

$SA=\int_{a}^{b}(2 \pi f(x)\; dx$

$SA=2 \pi \int_{a}^{b}f(x) \;dx$

$f(x)=r$
$SA=2 \pi r \int_{a}^{b}\;dx$

$SA=2 \pi r [x|_{a}^{b}=2 \pi (b-a)$

Si on prend $b-a=h$

On obtient:

$SA=2 \pi r h$

Surface latérale du cylindre engendré.

Exemples:

Trouver l’aire de la surface et le volume engendré par la rotation autour de l’axe des $y$ , de la portion de la courbe de $y=x^{2}$ sur l’intervalle $(1,1)$ et $(3,9)$

Solution

On peut utiliser:

$SA=\int_{a}^{b}(2 \pi g(y) \sqrt{1+(g'(y))^{2}}) \;dy$

$f(x)=x^{2}$

On peut dire que:

$x=\sqrt{y}$
$f'(y)=[\sqrt{y}]'=[(y)^{\frac{1}{2}}]'=\frac{1}{2 \sqrt{y}}$

$SA=\int_{1}^{9}2 \pi \sqrt{y}\sqrt{1+(\frac{1}{2 \sqrt{y}})^{2}} \;dy$

$SA=\int_{1}^{9}2 \pi \sqrt{y}\sqrt{1+\frac{1}{4y}} \;dy$

$SA=\int_{1}^{9}2 \pi \sqrt{y}\sqrt{\frac{4y+1}{4y}} \;dy$

$SA=\int_{1}^{9}2 \pi \sqrt{\frac{y(4y+1)}{4y}} \;dy$

$SA=\int_{1}^{9}2 \pi \sqrt{\frac{4y+1)}{4}} \;dy$

$SA=2 \pi \cdot \frac{1}{2}\int_{1}^{9} \sqrt{4y+1} \;dy$

$SA=\pi \int_{1}^{9} \sqrt{4y+1} \;dy$

Soit $4y+1=u^{2}\Rightarrow 2udu=4dy$

$dy=\frac{1}{2}udu$

$u^{2}=4y+1$

Quand $y=1$ on a $u=\sqrt{4 \cdot 1+1}=\sqrt{5}$

Quand $y=9$ on a $u=\sqrt{4 \cdot 9+1}=\sqrt{37}$

Nouvelle équation:

$SA=\pi \int_{1}^{9} \sqrt{4y+1} \;dy$

$SA=\pi \int_{\sqrt{5}}^{\sqrt{37}} u\cdot \frac{1}{2}u \;du$

$SA=\frac{\pi}{2} \int_{\sqrt{5}}^{\sqrt{37}} u^{2} \;du$

$SA=\frac{\pi}{2} \frac{u^{3}}{3} |_{\sqrt{5}}^{\sqrt{37}}$

$SA=\frac{\pi}{6} (37 \sqrt{37}-5\sqrt{5})\; sq.units$

Finalement:

$SA=\frac{\pi}{6} (37 \sqrt{37}-5\sqrt{5})\; sq.units$

$SA=35.647 \pi \; sq.units$

Trouver l’aire de la surface et le volume engendré par la rotation autour de l’axe des $x$ , la portion de la courbe de $y=\sqrt{x}$
sur l’intervalle $(1,1)$ et $(4,16)$

Solution

On peut utiliser:

$SA=\int_{a}^{b}(2 \pi f(x) \sqrt{1+(f'(x))^{2}}) \;dx$

$f(x)=\sqrt{x}$

On peut dire:

$f'(x)=[\sqrt{x}]'=[(x)^{\frac{1}{2}}]'=\frac{1}{2 \sqrt{x}}$

$SA=\int_{1}^{4}2 \pi \sqrt{x}\sqrt{1+(\frac{1}{2 \sqrt{x}})^{2}} \;dx$

$SA=\int_{1}^{4}2 \pi \sqrt{x}\sqrt{1+\frac{1}{4x}} \;dx$

$SA=\int_{1}^{4}2 \pi \sqrt{x}\sqrt{\frac{4x+1}{4x}} \;dx$

$SA=\int_{1}^{x}2 \pi \sqrt{\frac{x(4x+1)}{4x}} \;dy$

$SA=\int_{1}^{4}2 \pi \sqrt{\frac{4x+1)}{4}} \;dx$

$SA=2 \pi \cdot \frac{1}{2}\int_{1}^{4} \sqrt{4x+1} \;dx$

$SA=\pi \int_{1}^{4} \sqrt{4x+1} \;dx$

Soit $4x+1=u^{2}\Rightarrow 2udu=4dx$

$dx=\frac{1}{2}udu$

$u^{2}=4x+1$

Quand $x=1$ on a $u=\sqrt{4 \cdot 1+1}=\sqrt{5}$

Quand $x=4$ on a $u=\sqrt{4 \cdot 4+1}=\sqrt{17}$

La nouvelle équation:

$SA=\pi \int_{1}^{4} \sqrt{4x+1} \;dx$

$SA=\pi \int_{\sqrt{5}}^{\sqrt{17}} u\cdot \frac{1}{2}u \;du$

$SA=\frac{\pi}{2} \int_{\sqrt{5}}^{\sqrt{17}} u^{2} \;du$

$SA=\frac{\pi}{2} \frac{u^{3}}{3} |_{\sqrt{5}}^{\sqrt{17}}$

$SA=\frac{\pi}{6} (17 \sqrt{17}-5\sqrt{5})\; sq.units$

Finalement:

$SA=\frac{\pi}{6} (17 \sqrt{17}-5\sqrt{5})\; sq.units$

$SA=9.819 \pi \; sq.units$

Solides de revolution et volumes

Lorsqu’on tourne une courbe regulière autour d’un axe, on engendre un solide de revolution.

Si, par exemple, on prend un demi-cercle que l’on fait tourner autour de son axe, on engendre simplement une sphère.

En effectuant une rotation complète d’un segment de droite autour d’un axe parallèle , on engendre un cylindre.

Le cône quant à lui peut se créer par la revolution d’une droite de forme $y=kx$ autour de l’un des axes ( $x$ ou $y$ ).

Volume d’un cône:

Si on prend une droite $y=kx$ avec $k$ comme pente.

Nous savons déjà que $k=\tan \theta$ avec $\theta$ l’angle que forme la droite avec l’axe des $x$ .

Si l’on prend un point $B$ sur la droite, quand on effectue une revolution complète autour de l’axe des $x$ on observe clairement la reflection de $B$ autour de l’axe des $x$ qui est de $B'$ . La distance $BB'$ est le diamètre du cercle de centre $C$ sur l’axe des $x$ .

Le cône de sommet $O$ et de hauteur $OC$ est celui dont on peut trouver le volume de la façon suivante.

Si nous prenons deux points $M(x,y)$ et $N(x+\delta x, y+\delta y)$ sur la droite $y=kx$ , on voit qu’ils décrivent deux cercles après une revolution complète.

Quand ces deux points se rapprochent infiniment de façon à rendre $\delta x$ infiniment petit, $\delta x\rightarrow 0$ , le volume de la portionentre les deux cercles peut s’écrire:

$\pi y^{2}dx$

Soit $OC$ , $h$ la hauteur du cône. Quand on additionne ces petits volumes, on obtient le volume total de notre cône:

$V=\int_{0}^{h} \pi y^{2}\; dx$

Avec l’intégration:

$V=\frac{1}{3}\pi r^{2}h$ , with $r$ the radius of the base $r=OB$

Volumes des solides de revolution:

La méthode ci-dessus peut être utilisée pour n’importe quelle courbe:

La revolution autour de l’axe des $x$

$V=\int_{a}^{b} \pi y^{2}\; dx$

Exemple :

Calculer le volume du frustum, en utilisant le calcul intégral :

Effectuons la revolution de $y=kx+r$ autour de l’axe des $x$

$k$ est la tangente:

$k=\frac{R-r}{h}$

$y=\frac{R-r}{h}x+r$

Le volume:

$V=\int_{0}^{h} \pi y^{2}\; dx$

$y^{2}=(\frac{R-r}{h}x+r)^2$

$y^{2}=\frac{(R-r)^{2}}{h^{2}}x^{2}+\frac{2r(R-r)}{h}x+r^{2}$

Le volume :

$V=\int_{a}^{b} \pi y^{2}\; dx$

$V=\pi \int_{0}^{h} \frac{(R-r)^{2}}{h^{2}}x^{2}\;dx+\pi \int_{0}^{h} \frac{2r(R-r)}{h}x \;dx+\pi r^{2} \int_{0}^{h} \;dx$

$V=\pi \frac{(R-r)^{2}}{h^{2}} \frac{x^{3}}{3}|_{0}^{h}+\pi \frac{2r(R-r)}{h} \frac{x^{2}}{2} |_{0}^{h}+\pi r^{2} x |_{0}^{h}$

$V=\frac{\pi h}{3}(R^{2}-2Rr+r^{2})+\pi(rR-r^{2})h+\pi r^{2}h$

$V=\frac{\pi h}{3}(R^{2}-2Rr+r^{2})+=\frac{\pi h}{3}(3rR-3r^{2})+\frac{\pi h}{3}(3 r^{2})$

$V=\frac{\pi h}{3}( R^{2}-2Rr+r^{2}+3rR-3r^{2})$

$V=\frac{\pi h}{3}( R^{2}+Rr+r^{2})$

Finalement :

Le volume du Frustum est :

$V=\frac{\pi h}{3}( R^{2}+Rr+r^{2})$

Méthode des tranches

Méthode simple de calcul des volumes.

On cherche la forme de la section du solide.

On cherche la formule permettant de calculer l’aire de cette section et finalement on intègre sur l’intervalle qui couvre le solide.

C’est ce qu’on a utilisé dans le calcul des solides de revolution.

La méthode des disques:

On mesure l’aire sous la courbe et l’on la fait tourner autour de l’axe des $x$ .

On a vu cette méthode plus haut.

$V=\int_{a}^{b}\pi [f(x)]^{2}dx$

Ou autour de l’axe des $y$

$V=\int_{a}^{b}\pi [g(y)]^{2}dy$

Méthodes de disques troués:

Utilisée pour des solides ayant une cavité au milieu.

Le volume dans ce cas:

Si $f(x)$ et $g(x)$ sont continues, positives telles que $f(x) \geq g(x)$ sur $[a,b]$ . $A$ la région délimitée en haut par le graphe de $f(x)$ , et en bas par le graphe de $g(x)$ .

Vers la gauche délimitée par $x=a$ et vers la droite par la droite $x=b$ .

Le Volume:

$V=\int_{a}^{b}\pi [(f(x))^{2}-(g(x))^{2}]dx$

Exemple:
Trouver le volume obtenu par la rotation de laire entre les courbes $f(x)=x$ et $h(x)=\frac{1}{x}$ sur l’intervalle $[1,5]$

Le graphe montre une cavité au milieu, qui diminue quand on se rapproche de $x=5$

$V=\int_{a}^{b}\pi [(f(x))^{2}-(h(x))^{2}]dx$

$V=\int_{1}^{5}\pi [(x)^{2}-(\frac{1}{x})^{2}]dx$

$v=\pi \int_{1}^{5}[(x)^{2}-(\frac{1}{x})^{2}]dx$

$v=\pi (\frac{x^{3}}{3}+\frac{1}{x})|_{1}^{5}=\pi(\frac{125}{3}+\frac{1}{5}-\frac{1}{3}-1)=\frac{608 \pi}{15}$

Méthode des tubes

La région $R$ la région délimitée en haut par le graphe de la fonction $y=f(x)$ , en bas par l’axe des $x$ , sur la gauche et sur la droite par les droites $x=a$ and $x=b$ .

Une rotation autour de l’axe des $y$ donne un volume comme suit:

$V=\int_{a}^{b}(2 \pi x f(x)\;dx$

Post Views: 724

Calculs d’Intégrale

Calculs d’Intégrale

Théorème Fondamental du calcul intégral:

$\int_a^b f(x) \;dx= F(x)\Big |_a^b=F(b)- F(a)$

$\int_a^b c \;dx= c(b-a)$

$\int_a^b f(x) \;dx= \int_a^c f(x) \;dx +\int_c^b f(x) \;dx$

Théorème de la valeur moyenne:

Aires d’intégration:

Longeur d’une courbe:

$S=\int_a^b \sqrt{1+ (\frac{dy}{dx})^{2} } \cdot dx$

Théorème de Charles

Aire Totale:

Aires entre Courbes:

Aire composée entre deux courbes:

Régions complexes:

Solides de revolution et Surface des aires

Solides de revolution et volumes

Volume d’un cône:

Volumes des solides de revolution:

Méthode des tranches

La méthode des disques:

Méthodes de disques troués:

Méthode des tubes

Be the first to comment

Leave a Reply Cancel reply