The Definite Integral

After an extensive study of integration techniques, we are now ready to use the antiderivatives in practical situations.

The definite integral is used to calculate areas, lengths, volumes and other complicated things for normal methods of calculation.

We assume that the theory about Riemann Sums has been seen in the classroom and we start evaluating integrals right away.

Quick definition:Rienman Sum

If a function $f(x)$ is defined on the interval $[a,b]$ .

Definition:
Let $f(x)$ be defined on the closed interval $[a,b]$ and $\Delta$ be a partition of $[a,b]$
noted:
$a=x_{0}<x_{1}<x_{2}<x_{3}< \cdots <x_{n-1}<x_{n}=b$

Where $\Delta x_{i}$ is the width of the $ith$ subinterval.
If $c_{i}$ is any point in the $ith$ subinterval, then the sum:

$\sum_{i=1}^{n} f(c_{i}) \Delta x_{i}$

, $x_{i-1} \leq c_{i} \leq x_{i}$

This is the Riemann sum of $f$ for the partition $\Delta$

Now back to our topic.

Sir Isaac Newton and Gottfried Wilhelm Leibniz found an easy way to evaluate the integrals.

If $F$ is the antiderivative of a continuous function $f$ on the interval $[a,b]$ , we can write:

$\int_a^b f(x) \;dx= F(b)-F(a)$

This is also noted:

$\int_a^b f(x) \;dx= [F(x)]_a^b$

Fundamental Theorem of Integral Calculus:

If $a \leq x \leq b$ , and $F(x)$ is the indefinite integral of $f(x)$ :

$\int_a^b f(x) \;dx= F(x)\Big |_a^b=F(b)- F(a)$

We can now get the following properties:

$\int_a^b c \;dx= c(b-a)$

Example:

$\int_3^8 3 \;dx= 3(8-3)=15$

This is referred to an area under curve $y=3$ which happens to be a line.

We also have the following property:

$\int_a^b cf(x) \;dx= c\int_a^b f(x) \;dx$

Interval Union property:

If $a< c < b$ we can write:

$\int_a^b f(x) \;dx= \int_a^c f(x) \;dx +\int_c^b f(x) \;dx$

Average value theorem:

The average value of a function $f$ that has an antiderivative on $[a,b]$ the average of $f(x)$ is:

$\overline{y}=\frac{1}{b-a}\int_a^b f(x) \;dx$

Areas of integration:

Areas of integration can be seen as an area between two curves. If there is no second curve then the second function is simply $f(x)=0$ . It is said area under the curve in that case.

For Area both above and below the $x-axis$ , we have to subtract the negative area to make it positive.

Example:
We have two functions and we have to find the area enclosed by the two between the intersection points:

$f(x)=-x^{2}+6$

And

$g(x)=x$

We can simply write:

$<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-809a1a1efdb2b9338980ed7701ee8ad6_l3.png" height="196" width="504" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*}{\displaystyle \int \limits_{-3}^{2} (-x^{2}+6-x)\;dx}&= -\frac{x^{3}}{3}+6x-\frac{x^{2}}{2}\Big |_{-3}^{2}\\&=-\frac{2^{3}}{3}+6(2)-\frac{2^{2}}{2}-(-\frac{-3^{3}}{3}+6(-3)-\frac{-3^{2}}{2} \\&=-\frac{8}{3}+12-\frac{4}{2}-(\frac{27}{3}+6(-3)-\frac{9}{2})\\&=\frac{-16}{6}+\frac{114}{6}+\frac{27}{6}=\frac{125}{6}\end{align*}" title="Rendered by QuickLaTeX.com"/>$

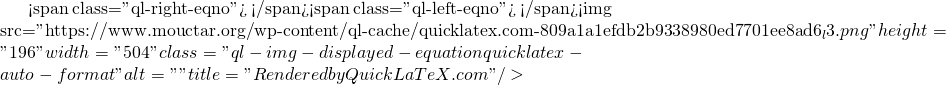
The length of curves

In our Geometry chapters, we have seen that the distance between two points $M(x_1,y_1)$ and $N(x_2,y_2)$ can be written:

$MN=\sqrt{(x_2-x_1)^{2}+ (y_2-y_1)^{2} }$

If we have a curve and we want to know the length between two points $A$ and $B$ , we can use the sum of the short chords like the chord $MN$ .

The shorter these chords, the closer we are to the actual length.

If we call $\delta x$ and $\delta y$ for the run and the rise, each small segment can have the length calculated using the distance formula.

$MN=\sqrt{(\delta x)^{2}+ (\delta y)^{2} }$

When $M$ and $N$ become so close that the value of $\delta x$ is close to $0$ , $\delta x \rightarrow 0$ , we can write: With $S=AB$

$MN=\sqrt{(dx)^{2}+ (dy)^{2} }$

$S=\int_a^b \sqrt{1+ (\frac{dy}{dx})^{2} } \cdot dx$

Finally, the length of the arc is noted:

$S=\int_a^b \sqrt{1+ (\frac{dy}{dx})^{2} } \cdot dx$

Example:
Given the circle $x^{2}+y^{2}=r^{2}$
Find the formulas for the area and the circumference using integral calculus.

Solution:

$x^{2}+y^{2}=r^{2}$

$y^{2}-r^{2}-x^{2}$

Implicit derivation:

$2y \frac{dy}{dx}=0-2x$

$2y \frac{dy}{dx}=-2x$

$\frac{dy}{dx}=-\frac{2x}{2y}$

$\frac{dy}{dx}=-\frac{x}{y}$

But :
$y=\sqrt{ r^{2}-x^{2}}$

We get :

$\frac{dy}{dx}=\frac{-x}{\sqrt{ r^{2}-x^{2}}}$

$(\frac{dy}{dx})^{2}=\frac{x^{2}}{r^{2}-x^{2}}$

For the Area:
If we consider the first Quadrant:

$A_{1}=\int_0^r \sqrt{r^{2}-x^{2}}\; dx$

Let $x=r \sin \theta$

$dx= r \cos \theta ; d \theta$

From above we have $\sin \theta=\frac{x}{r}$

For $x=0$

$\sin \theta=0 \Leftarrow \theta=0$

For $x=r$

$\sin \theta=\frac{r}{r}=1 \Leftarrow \theta=\frac{\pi}{2}$

Now the area is

$A_{1}=\int_{0}^{\frac{\pi}{2}} \sqrt{r^{2}-r^{2} \sin^{2} \theta} \cdot r \cos \theta \; d \theta$

$A_{1}=r\int_{0}^{\frac{\pi}{2}} \sqrt{1- \sin^{2} \theta} \cdot r \cos \theta \; d \theta$

$A_{1}=r^{2}\int_{0}^{\frac{\pi}{2}} \sqrt{ \cos^{2} \theta} \cdot \cos \theta \; d \theta$

$A_{1}=r^{2} \int_{0}^{\frac{\pi}{2}} \cos \theta \cdot \cos \theta \; d \theta$

$A_{1}=r^{2}\int_{0}^{\frac{\pi}{2}} \cos ^{2} \theta \; d \theta$

$A_{1}=r^{2}\int_{0}^{\frac{\pi}{2}} \frac{\cos 2\theta +1} {2} \; d \theta$

$A_{1}=\frac{r^{2}}{2}\int_{0}^{\frac{\pi}{2}} \cos 2\theta \; d \theta+ \frac{r^{2}}{2}\int_{0}^{\frac{\pi}{2}} d \theta$

$A_{1}=\frac{r^{2}}{2}\cdot \frac{1}{2} \sin 2\theta |_{0}^{\frac{\pi}{2}}+ \frac{r^{2}}{2} \cdot \frac{1}{2}\theta |_{0}^{\frac{\pi}{2}}$

$A_{1}=0-0+\frac{\pi r^{2}}{4}-0$

$A_{1}=\frac{\pi r^{2}}{4}$

Now since the circle has 4 quadrants:

$A=4A_{1}=\frac{\pi r^{2}}{4}$

$A=\pi r^{2}$

Finally the Area of the circle:

$A=\pi r^{2}$

For the circumference:

We use the same strategy and consider one quadrant:

$S_{1}= \int_{0}^{r} \sqrt{1+ (\frac{dy}{dx})^{2}} \;dx$

$S_{1}= \int_{0}^{r} \sqrt{1+ \frac{x^{2}}{r^{2}-x^{2}}} \; dx$

$S_{1}= \int_{0}^{r} \sqrt{ \frac{r^{2}-x^{2}+x^{2}}{r^{2}-x^{2}}} \; dx$

$S_{1}= \int_{0}^{r} \sqrt{ \frac{r^{2}}{r^{2}-x^{2}}} \; dx$

$S_{1}= r\int_{0}^{r} \sqrt{ \frac{1}{r^{2}-x^{2}}} \; dx$

$S_{1}= r \int_{0}^{r} \frac{dx}{\sqrt{r^{2}-x^{2}}}$

$S_{1}= r \sin^{-1} \frac{x}{r} |_{0}^{1}$

$S_{1}= r [\sin^{-1} (1)]- [\sin^{-1} (0)]$

$S_{1}= r \frac{\pi}{2}-0$

$S_{1}= \frac{r}{2} \pi$

For the 4 quadrants:

The circumference is:

$S= 4\frac{r}{2} \pi$

$S= 2 \pi r$

Finally:
The circumference is:

$S= 2 \pi r$

Net signed area

If we want to calculate the net signed area, we will have to calculate as follows:

Area Net=Area above $x-axis$ -Area below $x-axis$

If the integral is defined on interval $[a,b]$ and we have two areas $A_{1}$ above the $x-axis$ and $A_{1}$ below the $x-axis$ , the net signed area is:

$\int_{a}^{b} f(x)\;dx=A_{1}-A_{2}$

Example: Find the Net Signed Area between the curve of $f(x)=3x$ and the $x-axis$ over $[-2,2]$

We can calculate this by:

$\int_{-2}^{2}3x\;dx=6-6=0$

Total Area:

If the integral is defined on interval $[a,b]$ and we have two areas $A_{1}$ above the $x-axis$ and $A_{1}$ below the $x-axis$ , the net signed area is:

$\int_{a}^{b} f(x)\;dx=A_{1}+A_{2}$

This one is better found by checking the curve.

Areas between curves:

If $f(x)$ and $g(x)$ are two continuous functions over an interval $[a,b]$ and $f(x) \geq g(x)$ , the area between the curves is given by:

$A=\int_{a}^{b}[f(x)-g(x)]\; dx$

Example:

Find the area between the two following curve over interval $[1,3]$

$f(x)=2x+3$

$g(x)=-x+4$

The graph shows that $f(x) \geq g(x)$ over that interval:

$a= \int_{1}^{3}[f(x)-g(x)]\; dx= \int_{1}^{3}[(2x+3)-(-x+4)]\; dx=\int_{1}^{3}3x-1\; dx$

$\int_{1}^{3}3x-1\; dx=\int_{1}^{3}3x-\int_{1}^{3}dx=3\frac{x^{2}}{2}|_{1}^{3}-x|_{1}^{3}=\frac{3 \times 9}{2}-\frac{3 \times 1}{2}-3(1)+1(1)=12-3+1=10$

When the area between two curves is the bounded area , it is necessary to calculate the intersection points of the two curves.

Compound areas between curves:

When the curves cross in multiple points, it is necessary to examine the curves and compute the integrals as absolute values of the area.
$Area=\int_{a}^{b}|f(x)-g(x)|\;dx$

Complex Regions:

The following is bounded by the function $f(x)=\sqrt(x)$ and $g(x)=-x+5$

In this situation we split the integral at the intersection point.

Solids of revolution and Surface Areas

If f(x) is a nonnegative smoooth function over the interval $[a,b]$ .

Then, the surface area of the surface of revolution formed by revolving the graph of $f(x)$ around the $x-axis$ is given by:

$SA=\int_{a}^{b}(2 \pi f(x) \sqrt{1+(f'(x))^{2}}) \;dx$

If we take as $g(y)$ revolving aroung the $y-axis$

$SA=\int_{a}^{b}(2 \pi g(y) \sqrt{1+(g'(y))^{2}}) \;dy$

Example:

The line $f(x)=r$ is rotated around $x-axis$ over interval $[a,b]$
Find the surface area of the Surface of Revolution:

$SA=\int_{a}^{b}(2 \pi f(x) \sqrt{1+(f'(x))^{2}}) \;dx$

In this situation $f'(x)=0$

$SA=\int_{a}^{b}(2 \pi f(x)\; dx$

$SA=2 \pi \int_{a}^{b}f(x) \;dx$

$f(x)=r$
$SA=2 \pi r \int_{a}^{b}\;dx$

$SA=2 \pi r [x|_{a}^{b}=2 \pi (b-a)$

If we call $b-a=h$

We will have:

$SA=2 \pi r h$

This is simply the lateral area of the cylinder that has been generated.

Examples:

Find the surface area of the volume generated by revolving around the $y-axis$ , the portion of the curve of $y=x^{2}$ over interval $(1,1)$ and $(3,9)$

Solution

We can use:

$SA=\int_{a}^{b}(2 \pi g(y) \sqrt{1+(g'(y))^{2}}) \;dy$

$f(x)=x^{2}$

We cane say:

$x=\sqrt{y}$
$f'(y)=[\sqrt{y}]'=[(y)^{\frac{1}{2}}]'=\frac{1}{2 \sqrt{y}}$

$SA=\int_{1}^{9}2 \pi \sqrt{y}\sqrt{1+(\frac{1}{2 \sqrt{y}})^{2}} \;dy$

$SA=\int_{1}^{9}2 \pi \sqrt{y}\sqrt{1+\frac{1}{4y}} \;dy$

$SA=\int_{1}^{9}2 \pi \sqrt{y}\sqrt{\frac{4y+1}{4y}} \;dy$

$SA=\int_{1}^{9}2 \pi \sqrt{\frac{y(4y+1)}{4y}} \;dy$

$SA=\int_{1}^{9}2 \pi \sqrt{\frac{4y+1)}{4}} \;dy$

$SA=2 \pi \cdot \frac{1}{2}\int_{1}^{9} \sqrt{4y+1} \;dy$

$SA=\pi \int_{1}^{9} \sqrt{4y+1} \;dy$

Let $4y+1=u^{2}\Rightarrow 2udu=4dy$

$dy=\frac{1}{2}udu$

$u^{2}=4y+1$

When $y=1$ we get $u=\sqrt{4 \cdot 1+1}=\sqrt{5}$

When $y=9$ we get $u=\sqrt{4 \cdot 9+1}=\sqrt{37}$

Our new equation:

$SA=\pi \int_{1}^{9} \sqrt{4y+1} \;dy$

$SA=\pi \int_{\sqrt{5}}^{\sqrt{37}} u\cdot \frac{1}{2}u \;du$

$SA=\frac{\pi}{2} \int_{\sqrt{5}}^{\sqrt{37}} u^{2} \;du$

$SA=\frac{\pi}{2} \frac{u^{3}}{3} |_{\sqrt{5}}^{\sqrt{37}}$

$SA=\frac{\pi}{6} (37 \sqrt{37}-5\sqrt{5})\; sq.units$

Finally:

$SA=\frac{\pi}{6} (37 \sqrt{37}-5\sqrt{5})\; sq.units$

$SA=35.647 \pi \; sq.units$

Find the surface area of the volume generated by revolving around the $x-axis$ , the portion of the curve of $y=\sqrt{x}$
over interval $(1,1)$ and $(4,16)$

Solution

We can use:

$SA=\int_{a}^{b}(2 \pi f(x) \sqrt{1+(f'(x))^{2}}) \;dx$

$f(x)=\sqrt{x}$

We cane say:

$f'(x)=[\sqrt{x}]'=[(x)^{\frac{1}{2}}]'=\frac{1}{2 \sqrt{x}}$

$SA=\int_{1}^{4}2 \pi \sqrt{x}\sqrt{1+(\frac{1}{2 \sqrt{x}})^{2}} \;dx$

$SA=\int_{1}^{4}2 \pi \sqrt{x}\sqrt{1+\frac{1}{4x}} \;dx$

$SA=\int_{1}^{4}2 \pi \sqrt{x}\sqrt{\frac{4x+1}{4x}} \;dx$

$SA=\int_{1}^{x}2 \pi \sqrt{\frac{x(4x+1)}{4x}} \;dy$

$SA=\int_{1}^{4}2 \pi \sqrt{\frac{4x+1)}{4}} \;dx$

$SA=2 \pi \cdot \frac{1}{2}\int_{1}^{4} \sqrt{4x+1} \;dx$

$SA=\pi \int_{1}^{4} \sqrt{4x+1} \;dx$

Let

$4x+1=u^{2}\Rightarrow 2udu=4dx$

$dx=\frac{1}{2}udu$

$u^{2}=4x+1$

When $x=1$ we get $u=\sqrt{4 \cdot 1+1}=\sqrt{5}$

When $x=4$ we get $u=\sqrt{4 \cdot 4+1}=\sqrt{17}$

Our new equation:

$SA=\pi \int_{1}^{4} \sqrt{4x+1} \;dx$

$SA=\pi \int_{\sqrt{5}}^{\sqrt{17}} u\cdot \frac{1}{2}u \;du$

$SA=\frac{\pi}{2} \int_{\sqrt{5}}^{\sqrt{17}} u^{2} \;du$

$SA=\frac{\pi}{2} \frac{u^{3}}{3} |_{\sqrt{5}}^{\sqrt{17}}$

$SA=\frac{\pi}{6} (17 \sqrt{17}-5\sqrt{5})\; sq.units$

Finally:

$SA=\frac{\pi}{6} (17 \sqrt{17}-5\sqrt{5})\; sq.units$

$\mathbf {SA=9.819 \pi \; sq.units}$

Solids of revolution and volumes

When we rotate a regular curve or area about an axis, we get a solid of revolution.

Think about rotating a semi-circle about its axis, the space covered is simply a sphere.

The rectangle when rotated about one of the sides or a line segement rotated about a parallel line will describe a cylinder after a full rotation.

The cone is generated by rotating a line in the form of $y=kx$ about one axis ( $x$ or $y$ ).

Volume of the cone:

Let’s take the line $y=kx$ with $k$ being the slope.

We already know that $k=\tan \theta$ with $\theta$ being the angle that the line makes with the $x-axis$ .

If we take a point $B$ on the line, when we rotate the line around $x-axis$ for a complete revolution, we can clearly see that the reflection of $B$ about the $x-axis$ is $B'$ . The distance $BB'$ is the diameter of the circle with center $C$ on the $x-axis$ .

The cone with Apex $O$ and a height $OC$ is the one that the volume can be found using the following steps.

If we take two points $M(x,y)$ and $N(x+\delta x, y+\delta y)$ on the line $y=kx$ , they also describe two circles after the full revolution.

When these points become so close in such a way as to make $\delta x$ infinitely small, $\delta x\rightarrow 0$ , The volume of the slice between the two circles can be written:

$\pi y^{2}dx$

Let’s call $OC$ , $h$ the height of our cone. When we add all such small volumes, we get the volume of the full cone:

$V=\int_{0}^{h} \pi y^{2}\; dx$

An integration will simply yield :

$V=\frac{1}{3}\pi r^{2}h$ , with $r$ the radius of the base $r=OB$

Volumes of solids of revolution:

We can use the above method for any type of curve and we get the same results:

When rotated around $x-axis$

$V=\int_{a}^{b} \pi y^{2}\; dx$

Example :

Calculate the volume of a frustum, using integrals :

Let’s look at the figure and rotate $y=kx+r$ about $x-axis$

$k$ is the tangent:

$k=\frac{R-r}{h}$

$y=\frac{R-r}{h}x+r$

The volume:

$V=\int_{0}^{h} \pi y^{2}\; dx$

$y^{2}=(\frac{R-r}{h}x+r)^2$

$y^{2}=\frac{(R-r)^{2}}{h^{2}}x^{2}+\frac{2r(R-r)}{h}x+r^{2}$

The volume :

$V=\int_{a}^{b} \pi y^{2}\; dx$

$V=\pi \int_{0}^{h} \frac{(R-r)^{2}}{h^{2}}x^{2}\;dx+\pi \int_{0}^{h} \frac{2r(R-r)}{h}x \;dx+\pi r^{2} \int_{0}^{h} \;dx$

$V=\pi \frac{(R-r)^{2}}{h^{2}} \frac{x^{3}}{3}|_{0}^{h}+\pi \frac{2r(R-r)}{h} \frac{x^{2}}{2} |_{0}^{h}+\pi r^{2} x |_{0}^{h}$

$V=\frac{\pi h}{3}(R^{2}-2Rr+r^{2})+\pi(rR-r^{2})h+\pi r^{2}h$

$V=\frac{\pi h}{3}(R^{2}-2Rr+r^{2})+=\frac{\pi h}{3}(3rR-3r^{2})+\frac{\pi h}{3}(3 r^{2})$

$V=\frac{\pi h}{3}( R^{2}-2Rr+r^{2}+3rR-3r^{2})$

$V=\frac{\pi h}{3}( R^{2}+Rr+r^{2})$

Finally :

The volume of the Frustum is :

$V=\frac{\pi h}{3}( R^{2}+Rr+r^{2})$

Finding volumes by slicing

This is one of the simplest of the methods of finding a volume.

First we find out the shape of the cross-section of the solid.

Then we get the formula used to calculate the area of that section and finally we integrate over the interval covering the area.

This is the method we used to find the solid of revolution.

The disk method:

This consists of measuring the area under the curve and revolving it around the $x-axis$

We used the similar approach to calculate the volume of a solid of revolution.

$V=\int_{a}^{b}\pi [f(x)]^{2}dx$

or around the $y-axis$

$V=\int_{a}^{b}\pi [g(y)]^{2}dy$

The washer method:

This is the method used for solids with a cavities in the middle

The volume in that case:

If $f(x)$ and $g(x)$ are continuous, nonnegative such that $f(x) \geq g(x)$ over $[a,b]$ . $A$ is the region bounded above the graph $f(x)$ , below by the graph of $g(x)$ .

On the left it is bounded by $x=a$ and on the right by the line $x=b$ .

The Volume:

$V=\int_{a}^{b}\pi [(f(x))^{2}-(g(x))^{2}]dx$

Example:
Find the volume of the solid of revolution obtained by revolving the area between $f(x)=x$ and $h(x)=\frac{1}{x}$ over the interval $[1,5]$

The graph will show a cavity in the middle, reducing as we move towards $x=5$

$V=\int_{a}^{b}\pi [(f(x))^{2}-(h(x))^{2}]dx$

$V=\int_{1}^{5}\pi [(x)^{2}-(\frac{1}{x})^{2}]dx$

$v=\pi \int_{1}^{5}[(x)^{2}-(\frac{1}{x})^{2}]dx$

$v=\pi (\frac{x^{3}}{3}+\frac{1}{x})|_{1}^{5}=\pi(\frac{125}{3}+\frac{1}{5}-\frac{1}{3}-1)=\frac{608 \pi}{15}$

Cylindrical Shells

The region $R$ is bounded above by the graph of a function $y=f(x)$ , below by the $x-axis$ , and on the left and right by the lines $x=a$ and $x=b$ .

Now let’s revolve this region around the $y-axis$ .

The volume of the solid of revolution formed is:

$V=\int_{a}^{b}(2 \pi x f(x)\;dx$

Post Views: 248

The Definite Integral

The Definite Integral

Fundamental Theorem of Integral Calculus:

$\int_a^b f(x) \;dx= F(x)\Big |_a^b=F(b)- F(a)$

$\int_a^b c \;dx= c(b-a)$

$\int_a^b f(x) \;dx= \int_a^c f(x) \;dx +\int_c^b f(x) \;dx$

Average value theorem:

Areas of integration:

The length of curves

$S=\int_a^b \sqrt{1+ (\frac{dy}{dx})^{2} } \cdot dx$

Net signed area

Total Area:

Areas between curves:

Compound areas between curves:

Complex Regions:

Solids of revolution and Surface Areas

Solids of revolution and volumes

Volume of the cone:

Volumes of solids of revolution:

Finding volumes by slicing

The disk method:

The washer method:

Cylindrical Shells

Be the first to comment

Leave a Reply Cancel reply